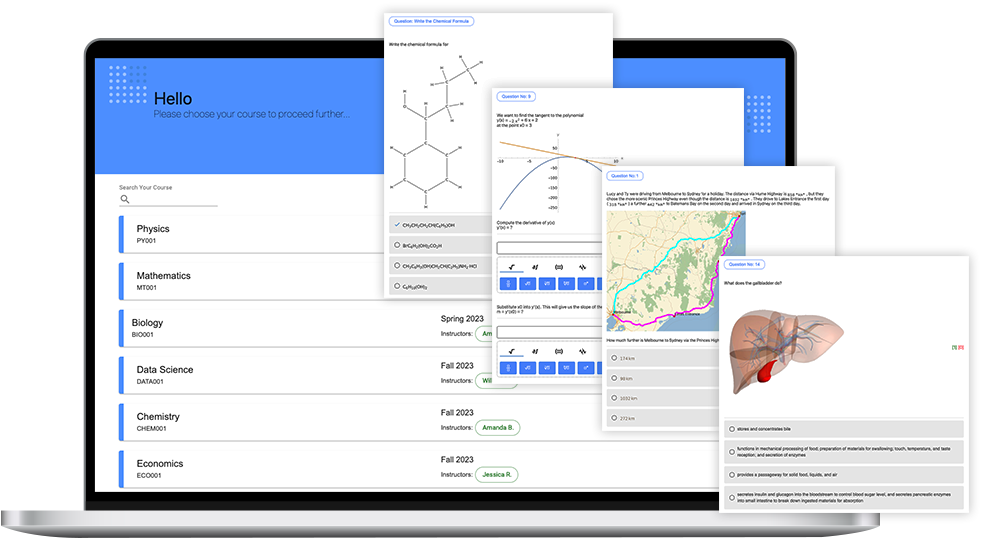
En quoi consiste Quezzio ?
Quezzio est une plateforme qui permet d'élargir les questions d'évaluation au-delà des manuels, de créer un contenu plus attrayant en incluant des figures intégrées et des expressions mathématiques typographiées, et d'offrir une notation précise pour tous les types d'évaluation.
Qui devrait adopter Quezzio ?
Les fournisseurs du secteur des technologies de l'éducation (EdTech) qui cherchent à améliorer leur environnement d'apprentissage en ligne
Quezzio offre une fonctionnalité mathématique améliorée, un soutien informatique pour le corps enseignant et des données du monde réel pour les évaluations.
Que comprend Quezzio ?
La plateforme comprend sept outils qui peuvent être combinés entre eux de manière transparente ou être utilisés sous licence en tant que composantes individuelles.
- Outil de création de questions
- Banque de questions
- Système de gestion de cours (CMS) /
système de gestion de l'apprentissage (LMS)
- Interface pour évaluer les étudiants
- Système de notation automatique
- Outil de saisie mathématique
- Analyses et rapports
Banque de questions et outil de création de questions
Générateur de problèmes Wolfram et questions pré-écrites supplémentaires
Le générateur de problèmes Wolfram fournit un nombre illimité de problèmes et de réponses de mathématiques pures générés par l'IA. En outre, la banque de questions est complétée par une bibliothèque de milliers de problèmes mathématiques pré-écrits, écrits et visuels, couvrant les cours du collège et du lycée, alignés sur les normes du tronc commun. Chaque question sert de modèle pour l'insertion de coefficients ou de fonctions aléatoires, ce qui permet de disposer d'un très grand nombre de questions différentes.
Notebook de modèles de questions
Utilisez des données réelles facilement disponibles pour créer de nouvelles questions et intégrer des graphiques pour n'importe quel domaine des STIM, y compris la chimie, la physique, les sciences de la terre, l'économie, le commerce et la finance.
Intégré dans votre CMS existant ou utilisé comme un CMS autonome

Banque de questions
Une fois créées, les questions sont téléchargées dans une banque de questions. Les questions peuvent ensuite être utilisées pour les devoirs, les QCM et d'autres supports de cours. Elles peuvent également être étiquetées, ce qui facilite leur localisation lors de la gestion d'une grande banque de questions dans différents cours et disciplines.
Intégration transparente avec les programmes CMS existants
Quezzio peut agir comme un CMS autonome ou être lié à un CMS existant comme Canvas, Blackboard, D2L ou Moodle. Vous pouvez créer les évaluations et les dates d'échéance pour des cours spécifiques et des listes d'étudiants.

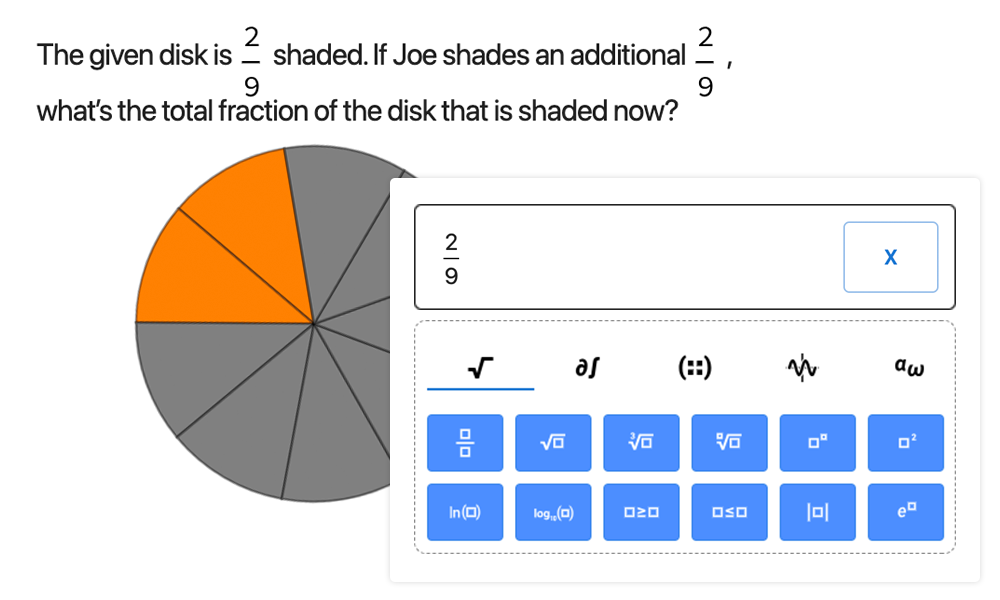
Interface d'évaluation des étudiants et outil de saisie des données mathématiques
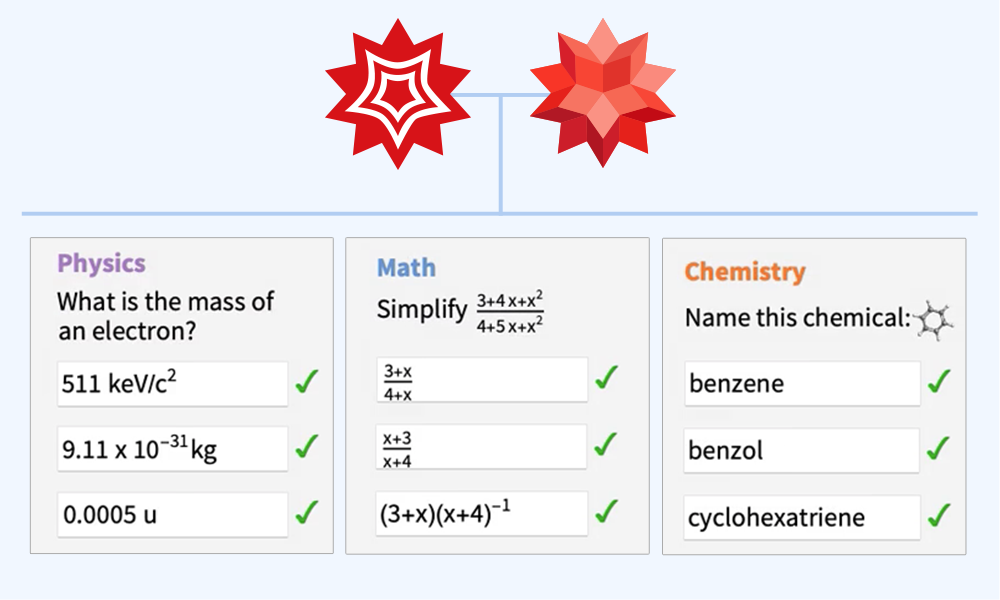
Une interface entièrement basée sur le web permet aux étudiants de faire leurs devoirs ou de répondre à des questions. Les réponses peuvent être facilement saisies sous forme d'expressions mathématiques typographiées afin d'éviter toute confusion ou ambiguïté.
Fonctionne avec le même moteur de notation automatique que Wolfram Mathematica et Wolfram|Alpha
Quezzio permet de noter automatiquement les réponses des étudiants de manière précise et fiable en s'appuyant sur la même technologie de base que celle qui fonde les principaux produits informatiques tels que Wolfram|Alpha et Mathematica.
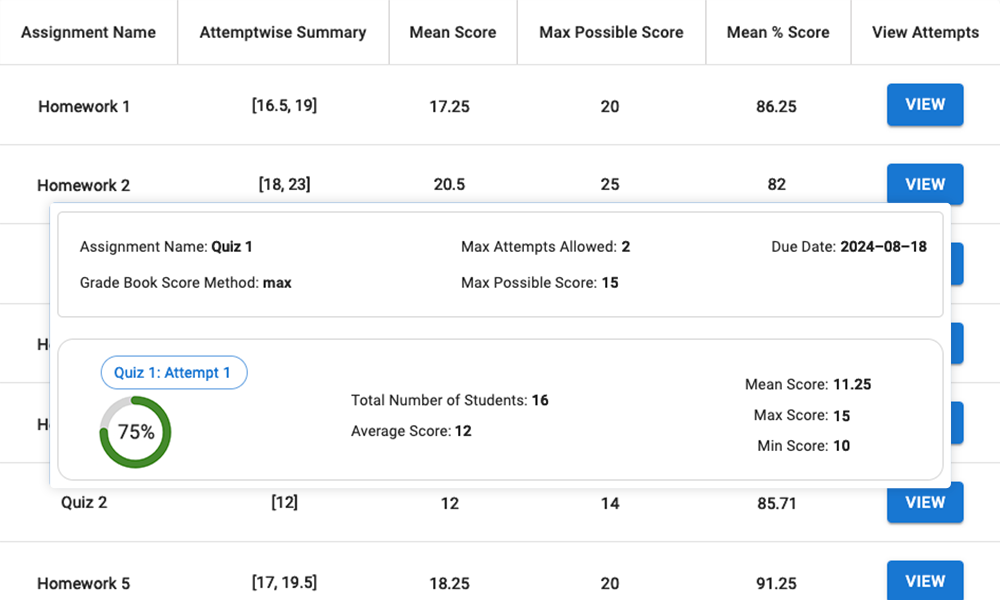
Rapports pour les enseignants
Les enseignants peuvent voir précisément le contenu des réponses des étudiants, ainsi que des résumés globaux pour chaque étudiant ou devoir. Les résultats peuvent être exportés vers un carnet de notes d'un CMS externe (comme Canvas).
FAQ
- Question. Ce système fonctionne-t-il avec notre système de connexion des étudiants (LTI, etc.) ? Réponse. Oui. Nous pouvons établir un lien avec votre système d'authentification afin de remplir automatiquement les listes de classe pour des cours spécifiques.
- Q. Wolfram propose-t-il une formation sur la création de questions ? R. Oui. Wolfram propose une formation personnalisée sur l'utilisation de Quezzio, ainsi que des services de conseil pour concevoir et mettre en œuvre une personnalisation sur mesure de la plateforme en fonction de vos besoins.
- Q. Wolfram héberge-t-il le système ou pouvons-nous l'héberger sur le campus ? R. L'un ou l'autre est possible. La plateforme peut fonctionner sur un serveur situé sur place, chez un fournisseur tiers de services en cloud ou sur les serveurs de Wolfram.
- Q. Le système exige-t-il que les étudiants sachent utiliser Mathematica ou coder en Wolfram Language ? R. Non. L'outil de création de questions fonctionne dans Mathematica, mais les étudiants ne voient pas de code en Wolfram Language lorsqu'ils font leurs devoirs ou répondent aux questions. Si le contenu du cours est centré sur l'enseignement de Mathematica et de Wolfram Language, les réponses des étudiants peuvent se présenter sous la forme de Wolfram Language et être notées automatiquement.
- Q. Quelle est la différence avec le générateur de problèmes Wolfram ? R. Le générateur de problèmes Wolfram est destiné à des questions d'entraînement anonymes, tandis que Quezzio permet d'intégrer ce type de technologie dans vos cours et vos systèmes de notation.
- Q. Cela remplace-t-il un LMS ou un CMS comme Canvas ? R. La plateforme peut agir comme un CMS autonome ou peut être liée à un CMS adopté comme Canvas pour fournir des évaluations et écrire dans le carnet de notes du CMS.