Простые числа Мерсенна и совершенные числа

Простое число Мерсенна - это простое число вида 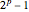, где показатель степени простого числа Мерсенна 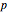сам является простым числом. Каждое простое число Мерсенна соответствует чётному совершенному числу.

Сгенерировать список показателей степени простого числа Мерсенна.

In[1]:=

mpe = Table[MersennePrimeExponent[n], {n, 1, 10}]

Out[1]=

Подобрать соответствующие простые числа Мерсенна.

In[2]:=

mp = 2^mpe - 1

Out[2]=

Подобрать соответствующие совершенные числа.

In[3]:=

pn = 2^(mpe - 1) (2^mpe - 1)

Out[3]=

In[4]:=

AllTrue[pn, PerfectNumberQ]

Out[4]=

Визуализирровать, насколько разреженным является распределение малых степеней простых чисел Мерсенна, обозначив их красным цветом в списке, состоящем из первых 225 простых чисел.

In[5]:=

primes = Replace[Prime@Range[225], x_?MersennePrimeExponentQ :> Style[x, Red, Bold], 1];

In[6]:=

Multicolumn[primes, Alignment -> {Center, Center}, Spacings -> {1, 1}, Frame -> All, FrameStyle -> Directive[Orange, Dashing[Small]]]

Out[6]=