Решение комбинаторной задачи с использованием постоянной
Постоянная схожа с детерминантой с различием в том, что все члены имеют положительный знак.
In[1]:=
Permanent[\!\(\*
TagBox[
RowBox[{"(", "", GridBox[{
{
SubscriptBox["a",
RowBox[{"1", ",", "1"}]],
SubscriptBox["a",
RowBox[{"1", ",", "2"}]]},
{
SubscriptBox["a",
RowBox[{"2", ",", "1"}]],
SubscriptBox["a",
RowBox[{"2", ",", "2"}]]}
},
GridBoxAlignment->{
"Columns" -> {{Left}}, "ColumnsIndexed" -> {},
"Rows" -> {{Baseline}}, "RowsIndexed" -> {}, "Items" -> {},
"ItemsIndexed" -> {}},
GridBoxSpacings->{"Columns" -> {
Offset[0.27999999999999997`], {
Offset[0.7]},
Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> {
Offset[0.2], {
Offset[0.4]},
Offset[0.2]}, "RowsIndexed" -> {}, "Items" -> {},
"ItemsIndexed" -> {}}], "", ")"}],
Function[BoxForm`e$,
MatrixForm[BoxForm`e$]]]\)]Out[1]=
In[2]:=
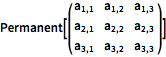
Permanent[\!\(\*
TagBox[
RowBox[{"(", "", GridBox[{
{
SubscriptBox["a",
RowBox[{"1", ",", "1"}]],
SubscriptBox["a",
RowBox[{"1", ",", "2"}]],
SubscriptBox["a",
RowBox[{"1", ",", "3"}]]},
{
SubscriptBox["a",
RowBox[{"2", ",", "1"}]],
SubscriptBox["a",
RowBox[{"2", ",", "2"}]],
SubscriptBox["a",
RowBox[{"2", ",", "3"}]]},
{
SubscriptBox["a",
RowBox[{"3", ",", "1"}]],
SubscriptBox["a",
RowBox[{"3", ",", "2"}]],
SubscriptBox["a",
RowBox[{"3", ",", "3"}]]}
},
GridBoxAlignment->{
"Columns" -> {{Left}}, "ColumnsIndexed" -> {},
"Rows" -> {{Baseline}}, "RowsIndexed" -> {}, "Items" -> {},
"ItemsIndexed" -> {}},
GridBoxSpacings->{"Columns" -> {
Offset[0.27999999999999997`], {
Offset[0.7]},
Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> {
Offset[0.2], {
Offset[0.4]},
Offset[0.2]}, "RowsIndexed" -> {}, "Items" -> {},
"ItemsIndexed" -> {}}], "", ")"}],
Function[BoxForm`e$,
MatrixForm[BoxForm`e$]]]\)]Out[2]=
Таким образом, применение Permanent для матрицы, все элементы которой равны 1 является интересным, но неэффективным способом вычисления функции факториала.
In[3]:=
Table[Permanent[ConstantArray[1, {n, n}]], {n, 10}]Out[3]=
Постоянная может использоваться для решения более интересных комбнаторных задач: даны n систем, каждая из которых содержит подсистему 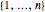 . Сколько существует способов нахождения определённого элемента из каждой подсистемы? Начнем с создания матрицы m, в которой положение (i, j) содержит 1, когда подсистема i содержит j, и 0 в противном случае.
. Сколько существует способов нахождения определённого элемента из каждой подсистемы? Начнем с создания матрицы m, в которой положение (i, j) содержит 1, когда подсистема i содержит j, и 0 в противном случае.
In[4]:=
sets = {{3, 5, 6, 7}, {3, 7}, {1, 2, 4, 5, 7}, {3}, {1, 3, 6}, {1, 5,
7}, {1, 2, 3, 6}}Out[4]=
In[5]:=
m = Table[If[MemberQ[sets[[i]], j], 1, 0] , {i, 7}, {j, 7}];
m // MatrixFormOut[5]//MatrixForm=

Постоянная m является решением задачи.
In[6]:=
Permanent[m]Out[6]=
Доказать результат, точно создав все наборы чисел.
In[7]:=
Select[Tuples[sets], DuplicateFreeQ]Out[7]=