極座標と球座標

直交座標と，2つの最も重要な非直交座標である極座標，球座標の間の変換を行うための関数が利用可能になった．

直交座標と極座標の間の変換を行う．

In[1]:=

ToPolarCoordinates[{x, y}]

Out[1]=

In[2]:=

FromPolarCoordinates[{r, \[Theta]}]

Out[2]=

直交座標と球座標の間の変換を行う．

In[3]:=

ToSphericalCoordinates[{x, y, z}]

Out[3]=

In[4]:=

FromSphericalCoordinates[{r, \[Theta], \[CurlyPhi]}]

Out[4]=

極座標は，自然に高次元に一般化される．

In[5]:=

ToPolarCoordinates[{w, x, y, z}]

In[6]:=

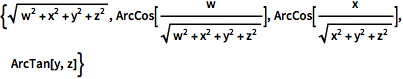
{Sqrt[w^2 + x^2 + y^2 + z^2], ArcCos[w/Sqrt[w^2 + x^2 + y^2 + z^2]], ArcCos[x/Sqrt[x^2 + y^2 + z^2]], ArcTan[y, z]}

In[7]:=

FromPolarCoordinates[{r, \[Theta]1, \[Theta]2, \[Theta]3, \ \[CurlyPhi]}]

Out[7]=

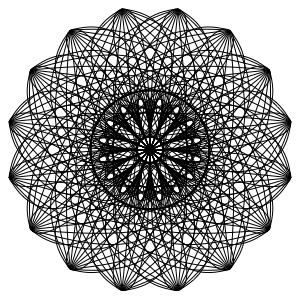
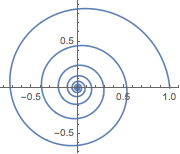
極座標と球座標で表された曲線をプロットする．

In[8]:=

ParametricPlot[ FromPolarCoordinates[{Exp[-t/10], t}] // Evaluate, {t, 0, 50}, PlotRange -> All]

Out[8]=

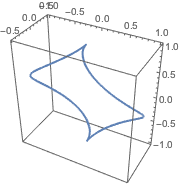
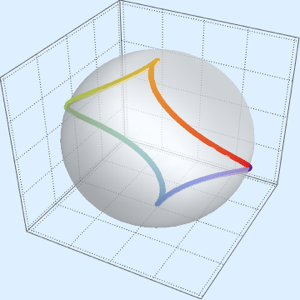
In[9]:=

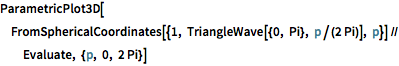
ParametricPlot3D[ FromSphericalCoordinates[{1, TriangleWave[{0, Pi}, p/(2 Pi)], p}] // Evaluate, {p, 0, 2 Pi}]

Out[9]=