Coordonnées polaires sphériques
De nouvelles fonctions dédiées sont disponibles pour convertir les coordonnées cartésiennes et les deux principaux systèmes de coordonnées non cartésiennes : les coordonnées polaires et les coordonnées sphériques.
Convertissez les coordonnées cartésiennes et les coordonnées polaires.
In[1]:=
ToPolarCoordinates[{x, y}]Out[1]=
In[2]:=
FromPolarCoordinates[{r, \[Theta]}]Out[2]=
Convertissez entre les coordonnées cartésiennes et les coordonnées sphériques.
In[3]:=
ToSphericalCoordinates[{x, y, z}]Out[3]=
In[4]:=
FromSphericalCoordinates[{r, \[Theta], \[CurlyPhi]}]Out[4]=
Les coordonnées polaires se généralisent naturellement à des dimensions supérieures.
In[5]:=
ToPolarCoordinates[{w, x, y, z}]Out[5]=
In[6]:=
FromPolarCoordinates[{r, \[Theta]1, \[Theta]2, \[Theta]3, \
\[CurlyPhi]}]Out[6]=
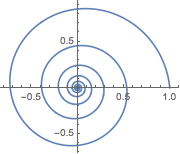
Tracez des courbes exprimées en coordonnées polaires et sphériques.
In[7]:=
ParametricPlot[
FromPolarCoordinates[{Exp[-t/10], t}] // Evaluate, {t, 0, 50},
PlotRange -> All]Out[7]=
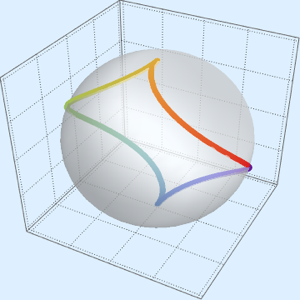
In[8]:=
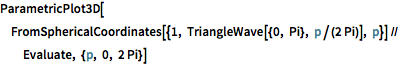
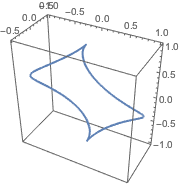
ParametricPlot3D[
FromSphericalCoordinates[{1, TriangleWave[{0, Pi}, p/(2 Pi)], p}] //
Evaluate, {p, 0, 2 Pi}]Out[8]=