셰퍼드 음： 착청: Wolfram Language 11의 신기능

셰퍼드 음： 착청

착청을 생성합니다.

In[1]:=

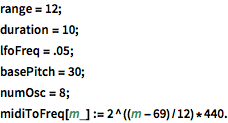
range = 12;
duration = 10;
lfoFreq = .05;
basePitch = 30;
numOsc = 8;
midiToFreq[m_] := 2^((m - 69)/12)*440.

진동의 주파수와 진폭을 제어하는 경사면을 생성합니다.

In[2]:=

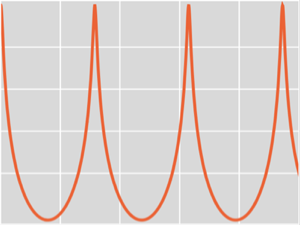
phasors = 
  Table[AudioGenerator[{"Sawtooth", lfoFreq, 2. Pi/numOsc (i - 1.)}, 
      duration, SampleRate -> 500]/2. + .5, {i, numOsc}];
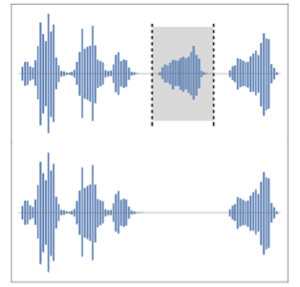
AudioPlot[phasors, PlotLayout -> "Overlaid", PlotRange -> All]

Out[2]=

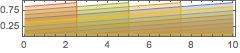
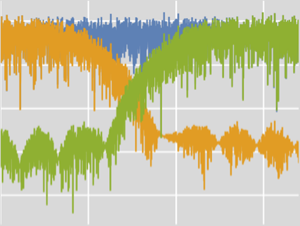
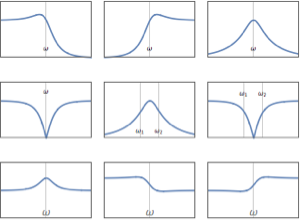
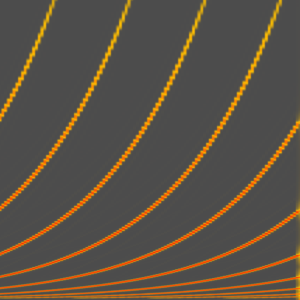
진동을 제어하는 주파수를 생성합니다. 주파수는 서로 정확히 한 옥타브 떨어져있고 기하 급수적으로 증가하기 때문에 피치는 선형으로 증가합니다.

In[3]:=

freqs = Table[
   midiToFreq[(phasors[[i]])*12*numOsc + basePitch], {i, numOsc}];
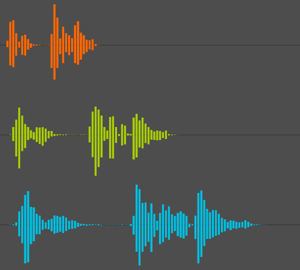
AudioPlot[freqs, PlotLayout -> "Overlaid", PlotRange -> All]

Out[3]=

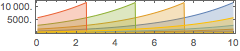
진동을 제어하는 진폭을 생성합니다. 진폭은 주파수가 최저값으로 떨어지면 0이 됩니다.

In[4]:=

amps = Cos[#*Pi - Pi/2.] & /@ phasors;
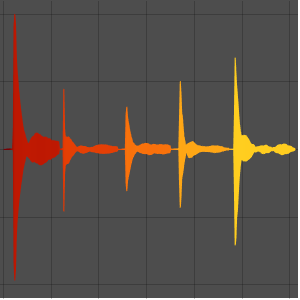
AudioPlot[amps, PlotLayout -> "Overlaid", PlotRange -> All]

Out[4]=

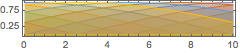
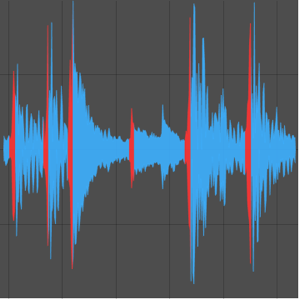
하나의 진동 주파수와 진폭 사이의 관계를 나타냅니다.

In[5]:=

AudioPlot[AudioNormalize /@ {freqs[[2]], amps[[2]]}, PlotRange -> All]

Out[5]=

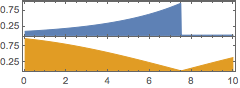
생성된 주파수와 진폭을 사용하여 진동의 경사면을 결합합니다.

In[6]:=

res = Mean[
  Table[amps[[i]] AudioGenerator[{"Sin",  freqs[[i]]}], {i, numOsc}]]

Out[6]=

In[7]:=

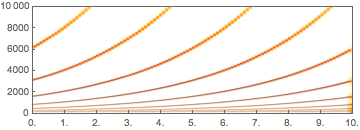
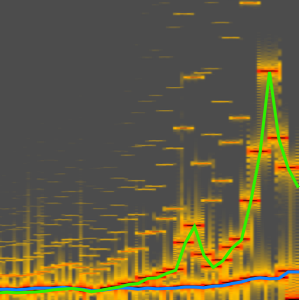
Spectrogram[res, 8192, 4096, HannWindow, 
 PlotRange -> {All, {0, 10000}}, ImageSize -> Medium]

Out[7]=

Wolfram 언어™

셰퍼드 음： 착청

관련 예제