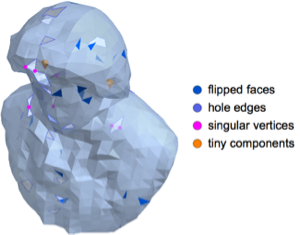
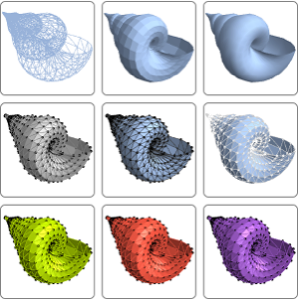
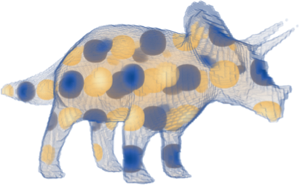
Équations aux dérivées partielles symboliques sur les régions

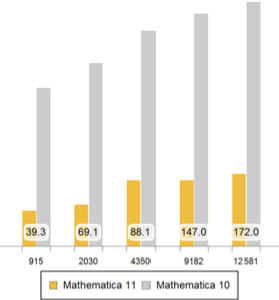
La version 11 ajoute une prise en charge élargie pour les solutions symboliques et numériques de problèmes aux limites sur les régions.

Le problème de Dirichlet pour l'équation de Laplace dans un disque.

In[1]:=

leqn = Laplacian[u[x, y],{x, y}] == 0;

In[2]:=

dcond = DirichletCondition[u[x, y] == Sin[6 ArcTan[y/x]], True];

In[3]:=

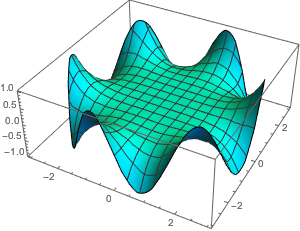
\[CapitalOmega] = Disk[{0, 0}, 3];

Résolvez symboliquement 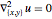dans une une unité de disque avec la condition aux limites de Dirichlet.

In[4]:=

sol = DSolveValue[{leqn, dcond}, u[x, y], {x, y} \[Element] \[CapitalOmega]]

Out[4]=

In[5]:=

Plot3D[sol, {x, y} \[Element] \[CapitalOmega], PlotRange -> All, PlotStyle -> Hue[0.5], Exclusions -> None]

Out[5]=