영역에서 기호적 편미분 방정식

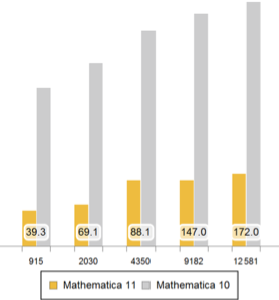
버전 11은 영역에서의 경계 값 문제의 기호 해석 및 수치 해석의 광범위한 지원을 추가하였습니다.

원판에서의 라플라스 방정식의 디리클레 문제를 살펴봅니다.

In[1]:=

leqn = Laplacian[u[x, y],{x, y}] == 0;

In[2]:=

dcond = DirichletCondition[u[x, y] == Sin[6 ArcTan[y/x]], True];

In[3]:=

\[CapitalOmega] = Disk[{0, 0}, 3];

단위 원판상의 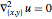을 디리클레 경계 조건으로 해결합니다.

In[4]:=

sol = DSolveValue[{leqn, dcond}, u[x, y], {x, y} \[Element] \[CapitalOmega]]

Out[4]=

In[5]:=

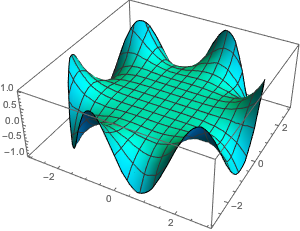
Plot3D[sol, {x, y} \[Element] \[CapitalOmega], PlotRange -> All, PlotStyle -> Hue[0.5], Exclusions -> None]

Out[5]=