不規則にサンプリングされた確率過程の推定: Wolfram言語 11の新機能

不規則にサンプリングされた確率過程の推定

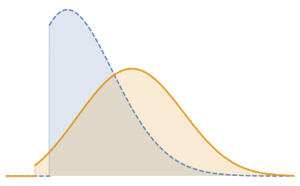
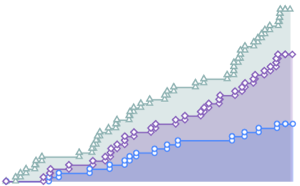
不規則にサンプリングされたOrnsteinUhlenbeckProcessの実現を生成する．

In[1]:=

sample = TimeSeriesResample[
  RandomFunction[
   OrnsteinUhlenbeckProcess[0, .1, .3], {0, 100, .1}], {Sort[
    RandomReal[100, 1000]]}]

Out[1]=

完全なWolfram言語入力を表示する

In[2]:=

ListLinePlot[sample, Filling -> Axis, ImageSize -> Medium, 
 PlotTheme -> "Detailed"]

Out[2]=

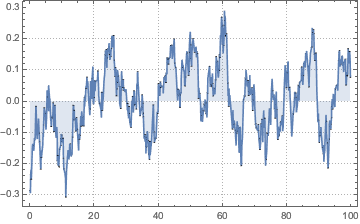
不規則にサンプリングされたデータから過程母数を推定する．

In[3]:=

EstimatedProcess[sample, 
 OrnsteinUhlenbeckProcess[\[Mu], \[Sigma], \[Theta]]]

Out[3]=

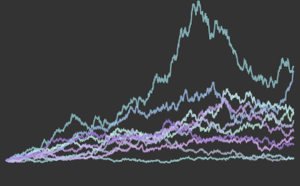
2013年1月1日以降のGEの株価を取り出し，それをTemporalDataに変換する．

In[4]:=

price = TemporalData[FinancialData["GE", "Jan. 1, 2013"]]

Out[4]=

完全なWolfram言語入力を表示する

In[5]:=

DateListPlot[price, Filling -> Axis, ImageSize -> Medium, 
 PlotTheme -> "Detailed"]

Out[5]=

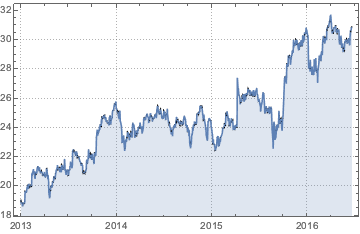
株価データのタイムスタンプは一様ではない．

In[6]:=

MinMax[Differences[price["Times"]]]

Out[6]=

対数価格がFractionalBrownianMotionProcessを満足すると仮定して，母数を推定する．

In[7]:=

EstimatedProcess[Log[price], 
 FractionalBrownianMotionProcess[\[Mu], \[Sigma], h]]

Out[7]=