Язык Wolfram Language™

Оценка нерегулярных выборок случайных процессов

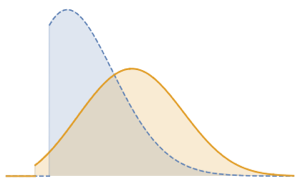
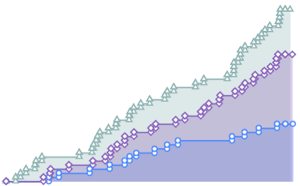
Сформируем нерегулярную выборку с помощью функции OrnsteinUhlenbeckProcess.

In[1]:=

sample = TimeSeriesResample[ RandomFunction[ OrnsteinUhlenbeckProcess[0, .1, .3], {0, 100, .1}], {Sort[ RandomReal[100, 1000]]}]

Out[1]=

In[2]:=

ListLinePlot[sample, Filling -> Axis, ImageSize -> Medium, PlotTheme -> "Detailed"]

Out[2]=

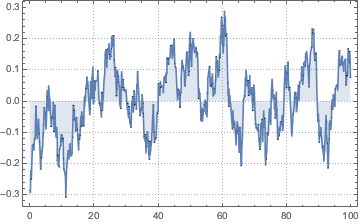
Вычислим параметры процесса на основе нерегулярных выборок данных.

In[3]:=

EstimatedProcess[sample, OrnsteinUhlenbeckProcess[\[Mu], \[Sigma], \[Theta]]]

Out[3]=

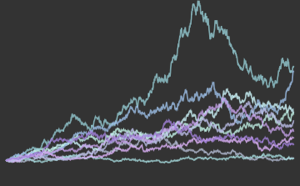
Возьмем цены на акции компании General Electric с 1 января 2013 года, и конвертируем их в временные ряды с помощью функции TemporalData .

In[4]:=

price = TemporalData[FinancialData["GE", "Jan. 1, 2013"]]

Out[4]=

In[5]:=

DateListPlot[price, Filling -> Axis, ImageSize -> Medium, PlotTheme -> "Detailed"]

Out[5]=

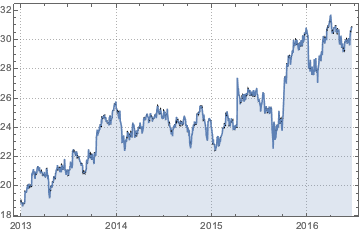
Штамп времени данных о ценах акций неоднороден.

In[6]:=

MinMax[Differences[price["Times"]]]

Out[6]=

Предположим, что логарифм цены соответствует характеристикам дробного броуновского движения (см. FractionalBrownianMotionProcess) и вновь вычислим параметры процесса.

In[7]:=

EstimatedProcess[Log[price], FractionalBrownianMotionProcess[\[Mu], \[Sigma], h]]

Out[7]=