‹›拡張された確率と統計の機能分布特性の計算の高速化
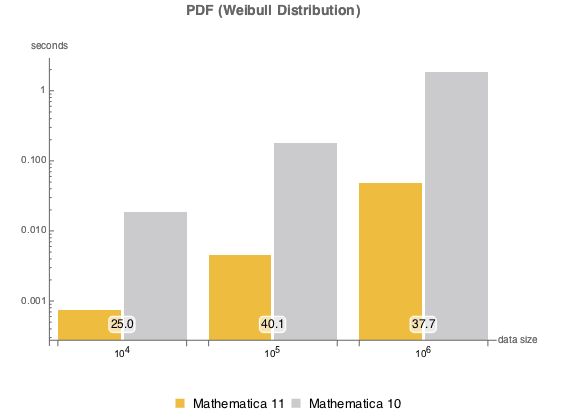
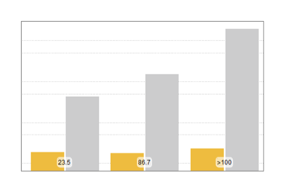
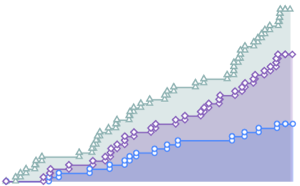
バージョン11では,広範に渡る分布特性の数値計算が拡張されている.以下のグラフは,さまざまなサンプルサイズについて計算速度を比べたものである.実験は,Intel Xeon Processor E3-1245 v2 3.40 GHzを搭載したWindows 10のシステムを使って行われた.一番下の数字は,バージョン11がバージョン10と比べてどのくらい速いかを示す.
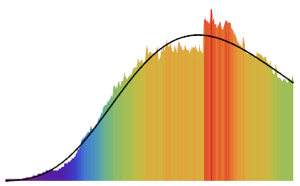
確率密度関数についてリストがより作成しやすくなった.
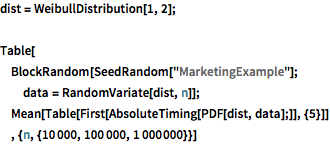
完全なWolfram言語入力を表示する
dist = WeibullDistribution[1, 2];
Table[
BlockRandom[SeedRandom["MarketingExample"];
data = RandomVariate[dist, n]];
Mean[Table[First[AbsoluteTiming[PDF[dist, data];]], {5}]]
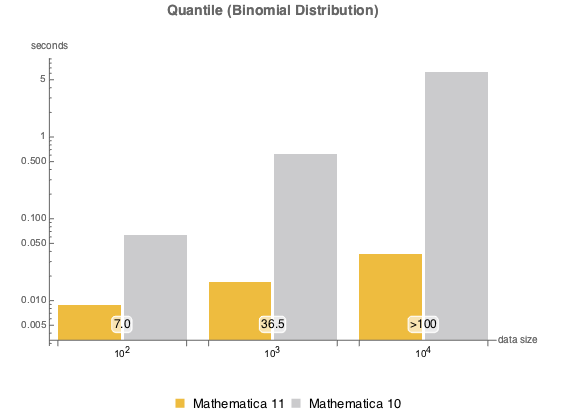
, {n, {10000, 100000, 1000000}}]離散分布の分位点の計算がより高速になった.
完全なWolfram言語入力を表示する
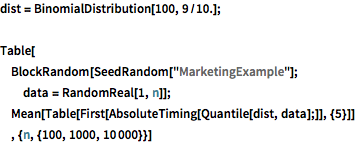
dist = BinomialDistribution[100, 9/10.];
Table[
BlockRandom[SeedRandom["MarketingExample"];
data = RandomReal[1, n]];
Mean[Table[First[AbsoluteTiming[Quantile[dist, data];]], {5}]]
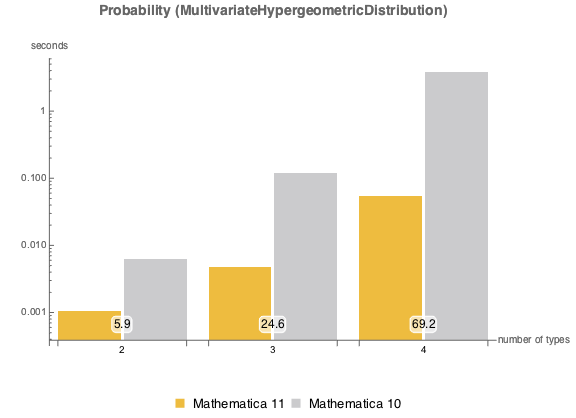
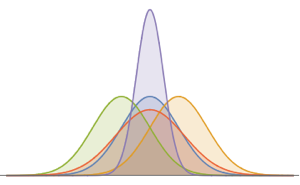
, {n, {100, 1000, 10000}}]多変量超幾何分布の確率.
完全なWolfram言語入力を表示する
Table[
Mean[Table[First[AbsoluteTiming[TimeConstrained[
BlockRandom[SeedRandom["MarketingExample"];
symbols = Table[Unique[a], {n}];
Probability[Min[symbols] >= 2 && Max[symbols] <= 12,
symbols \[Distributed]
MultivariateHypergeometricDistribution[30,
RandomInteger[{20, 40}, n]]];
], 100]]], {5}]], {n, {2, 3, 4}}]