Durée de voyage et distance
Faites l'estimation de la distance et de la durée d'un voyage sur la route.
Voyagez entre deux villes éloignées.
In[1]:=
cities = {Entity["City", {"Lisbon", "Lisboa", "Portugal"}],
Entity["City", {"Beijing", "Beijing", "China"}]};Voici la distance géodésique entre elles.
In[2]:=
GeoDistance[cities]Out[2]=
Voici la longueur du voyage sur la route calculée.
In[3]:=
TravelDistance[cities]Out[3]=
Et voici le temps de conduite estimée, en supposant que la conduite est continue et sans arrêt.
In[4]:=
TravelTime[cities]Out[4]=
Cet objet contient l'ensemble réel des consignes de voyage.
In[5]:=
td = TravelDirections[{Entity[
"City", {"Lisbon", "Lisboa", "Portugal"}],
Entity["City", {"Beijing", "Beijing", "China"}]}]Out[5]=
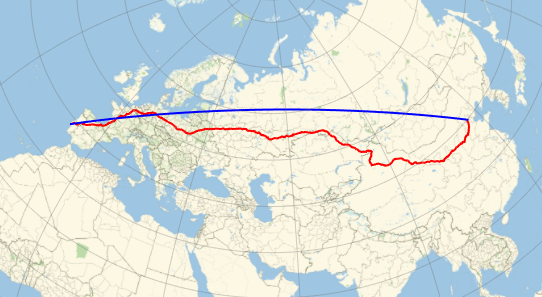
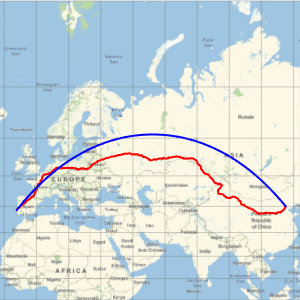
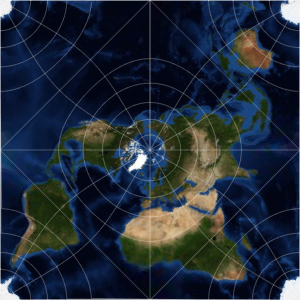
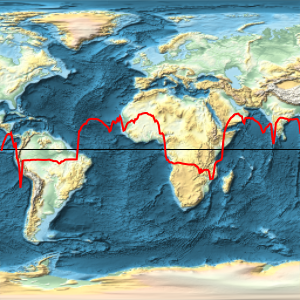
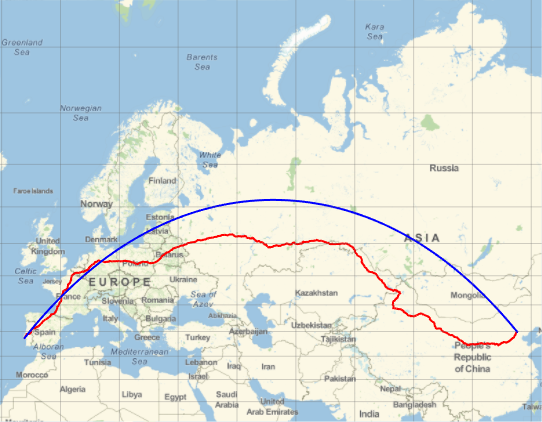
Représentez la trajectoire (en rouge) sur une projection de Mercator, et comparez-la à la trajectoire géodésique (en bleu) ce qui est en fait plus courte, comme nous avons remarqué précédemment.
In[6]:=
GeoGraphics[{Thick, Red, GeoPath[td], Blue,
GeoPath[{Entity["City", {"Lisbon", "Lisboa", "Portugal"}],
Entity["City", {"Beijing", "Beijing", "China"}]}]},
GeoProjection -> "Mercator", GeoGridLines -> Automatic]Out[6]=
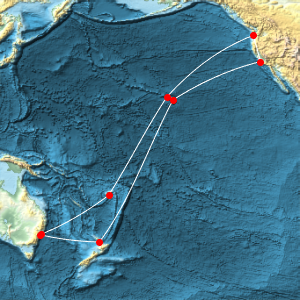
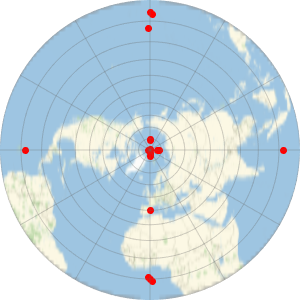
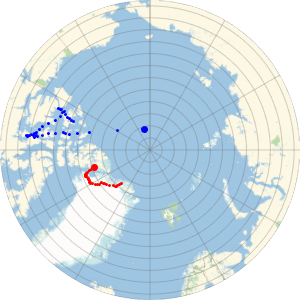
Une projection azimutale montre plus clairement que la ligne géodésique est plus courte que le trajet de voyage.
In[7]:=
GeoGraphics[{Thick, Red, GeoPath[td], Blue,
GeoPath[{Entity["City", {"Lisbon", "Lisboa", "Portugal"}],
Entity["City", {"Beijing", "Beijing", "China"}]}]},
GeoProjection -> "Mercator", GeoGridLines -> Automatic];
Show[%, GeoProjection -> "LambertAzimuthal", GeoZoomLevel -> 4]Out[7]=
