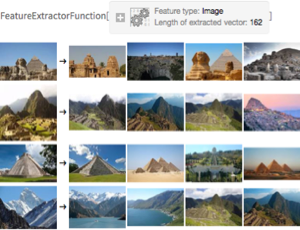
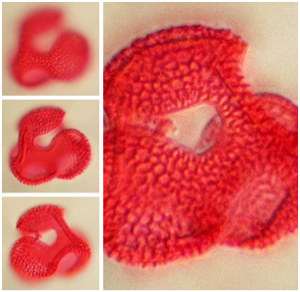
다각도의 재구축
삼차원 객체는 다각도의 이차원 관점으로부터 재구축이 가능합니다. ImageDisplacements는 하나의 시점에서 다른 시점으로의 변위 파악에 사용됩니다. 시차의 변화가 클수록 해당 픽셀의 뒤 객체에 의해 가까워집니다. 이 심도 정보를 바탕으로 ImageMesh와 TriangulateMesh에서 얻을 수 있는 객체 메쉬의 정점을 밀어낼 수 있습니다. 결과는 삼차원 메쉬 오브젝트에 텍스처 매핑으로 표시됩니다.
In[1]:=

중앙 이미지의 객체 마스크를 얻습니다.
In[2]:=
mask = Erosion[Binarize[imgs[[2]], 0], 1];중앙 이미지에 대응하는 왼쪽과 오른쪽 이미지의 시차를 구합니다.
In[3]:=
parallaxL = First@ImageDisplacements[imgs[[{2, 1}]]];In[4]:=
parallaxR = First@ImageDisplacements[imgs[[{2, 3}]]];시차의 합계에 이러한 변위를 결합합니다.
In[5]:=
parallax = parallaxL - parallaxR;지정된 설정에서 시차 ![]() 의 성분은 대응하는 화소원의 심도에 대체로 비례합니다.
의 성분은 대응하는 화소원의 심도에 대체로 비례합니다.
In[6]:=
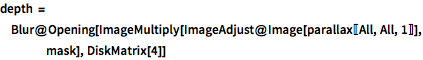
depth = Blur@
Opening[ImageMultiply[ImageAdjust@Image[parallax[[All, All, 1]]],
mask], DiskMatrix[4]]Out[6]=

심도 함수를 구축합니다.
In[7]:=
depthFunction = ListInterpolation[Transpose@Reverse@ImageData[depth]];객체의 돌출에 의해 세분화된 객체 메쉬를 얻습니다.
In[8]:=
resolution = ImageAdjust@ImageSaliencyFilter[imgs[[2]]];In[9]:=
resolutionFunction =
ListInterpolation[Transpose@Reverse@ImageData@resolution];In[10]:=

\[CapitalOmega] = TriangulateMesh[
ImageMesh[Erosion[mask, DiskMatrix[2]]],
MeshRefinementFunction ->
Function[{vertices, area},
area > 32 + 512 (1 - resolutionFunction @@ Mean[vertices])^6]
]Out[10]=
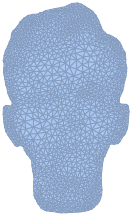
객체 메쉬를 심도 함수로 밀어냅니다.
In[11]:=

Graphics3D[
GraphicsComplex[
Apply[{##, depthFunction[##]} &,
MeshCoordinates[\[CapitalOmega]], {1}],
{EdgeForm[], MeshCells[\[CapitalOmega], 2]}
],
PlotRange -> Append[Thread[{0, ImageDimensions[mask]}], {0, 1}],
BoxRatios -> {1, 1, 2/3},
ViewPoint -> Top
]Out[11]=

객체의 텍스처를 중앙 이미지에서 추출합니다.
In[12]:=
texture = SetAlphaChannel[imgs[[2]], mask]Out[12]=

텍스처를 삼차원 객체에 매핑합니다.
In[13]:=

Graphics3D[
{Texture[texture],
GraphicsComplex[
Apply[{##, depthFunction[##]} &,
MeshCoordinates[\[CapitalOmega]], {1}],
{EdgeForm[], MeshCells[\[CapitalOmega], 2]},
VertexTextureCoordinates ->
Map[#/ImageDimensions[texture] &, MeshCoordinates[\[CapitalOmega]]]
]
},
PlotRange -> Append[Thread[{0, ImageDimensions[mask]}], {0, 1}],
BoxRatios -> {1, 1, 2/3},
Lighting -> {{"Ambient", White}},
ViewPoint -> Top,
Boxed -> False
]