DateHistogram의 날짜 비닝
모멘트 규모가 6보다 큰 지진의 시계열을 알아봅니다.
In[1]:=
ed = TemporalData[TimeSeries, {CompressedData["
1:eJyVmt2NI0cMhNt+cAx70oykdQqXwMZwEQgGfK+O596cgVPYAC4o60ENFT9V
sXULLBqj6R82u0gW2fP+1z/f/v59jPHb7f+/P8b97+1D2uv37+V5th9fv37R
9vPnz9J//v7vjx9f9PfZL63D9eY8jTxbN17W3cL4N5WT+0j9V+P4LPs56vPs
R73wWeQ5QI7yPPXFdW/zlX43uYscbCmX7Ivrt+dIOaa+0nqchzia+51ySEs5
T5iX++e8Fm9s5/kl+WS+S6efOQ/xQHviuBXOef4JVytcr86Pdp3kXs0r8x+c
3Ct9vOpniF9jl2cn75wn4WUE3PCZ+L2tX/Ah+92dvDxX7jP5kRVuRM5iTzL+
hPEHjGv9Bs9xhdMVrnnO3IfB9ZS32BnXTefKfaV4JDi1+OI8A7igXk08Pd77
n7W9vd9e0ff099wv48nt913Xm3gUv3dw6yW9Jf9h4lM5L+oxxZ2EQ+KdcVrw
tN/HFT1yfupN9Nue96vtivekfSV9JH/VnFt7rq/OM3FGfVO+1E48r/Zr/Fyx
c7Gb1q9zvOEZFp/UC+1fcEaeZfkK7TDFPeqLv1Mu4//t+uPBow9okz8+uveG
r1k/meQU/Z7wu92/6KfgZuCcZd0t/G7P9wUecrq/3/E75Zj42qEfxlsrx6/6
l5nvjLseU79f9TOi/7mPo7amH/Fa8MV90q/Kc7uPATwZnEz9H9HauN3kc9Y+
Ei9IfC2ds+h11/7cB/c7gNckh/H70x6K/1vlbSveNp7Psz0n4TPTns46LvFf
GV/4zUpOaTe05XxnHjnlSrxJ1rN5dsrbk78U/ZR9GfzNebf7OOYP1n/x9+Qf
k77Hs/+4YNxJ36f4PIBbEweLvd6eL5j/fG93bU39ouhp5Dhs8UM5Tb5g86LE
G1d1BqOXFseJh4tfbuMj+Qrtqanbka9vOs+MQ/Rb5FOr/JLyvVrHMPqw9aRV
HSide9JLOudVf8ZF0V+pX7J+ZOKarTMyDo+AC8PLLW4G7Gg8cGH3ZfJlizvK
Mx7+7b3To/hbux/Kl+ZJ+ZGZp/hhOZe2HiX2leK5zX/FzpI90S43PM/+039a
eV+wf2s3Jk6k+qzN86hn4WebPr9ghyeMLzii/ow/tfUYI1fyZ+W8JH7t6E87
ob/Zdd6B801+xuip6NvkK1O/xINdJ+nDxFGeZ+Enqd6V6ogTB6nOseKLYkcz
nzjhfYrvdl7yGbFnm0+Mh93sOt+AnRAnJj4U3sr3hqfaOLLiO8Z+Cq65fzNf
0QN50AjxxPivJCfzyD91HWlLvbSpP7U4HDjXAX9oeKe11xRPqc/ESxr52niW
4qLJiyyOUl4r8Tv5AYsn5t/Up+RljGsWD8mvJz7EfoKHtv8I9r3i98YuU5y3
fu76XAcpcdHow+Ihxa8m7h3x3OaT10cdl3GH8xzxO8+XvNf6ubHAufGrZZ1U
t07xLPkjiW+WVzO+cv2GX7bxifIZfBc8cf6P5/sdyxubvIx+NPE7xkmLS/Yz
eii8KvlDOY/iT7iu2c875J/3tRY3KR9inGQ9osmL7fOK96b5Ep9JcYbvE+8z
cnFf1h8b/Nt4LPZ6cuMEv7ynLPxf1rf3CgY3jLstb09xLMWNZj8FtyYetXnX
wHkY3pV4ZfIPxU/LPtL9zCpuWr2l+4NxrysyniQ/ZPhWqX+xHst4kvy+4RHE
t+VHKz0wzjX++azPJn9O69t4MB55mb2fpJzjgauCy9vzRecxeVxb91vxxY/H
9zDFzo18dv9J74Yvtvc/A3XjxP9H1jfXT/JOflfqqAN+NcUBU8cp9ZPrc33W
xkXGL+pptQ/BSbnHMfqy/DXlgykfTfaa3o9n+7X2/ZnvBVkXKfyReZypGzBe
8PuT1m5lX5OXXLr+E1e8V1zl/2J/Bf/kiybPL/c0XF/O097bkX8KPy54Mn7b
8ioj78ovlHHpvmc8+wPqo/UHiUeyfsF8UPqV71tSPPtE/ZT2n/ipmc/ai+EP
Zd6UDyd9pPsAyiX7snWoVRw2967td4ImP7Xzih4LjslrWQ819mjtQPpvOt/n
8z1Birs2Dx+hPj5gRyZfLOut6kppP8IrbHwiTs25lHlX9UbZZ6kzGH9CvJTv
AhinDa96c+/T9wRJj/TbhhfaPNmcW/k+6Pr4jrTgqamHWf+a7iG5flNfKnx3
xd+MfgtfY176Ql3O8inG6fHMHwp/MvewLb5oD4ZH0O/a94b/ze+FL90+k75Y
DxzPfrr0N3ww8aeCs3HHYcJFqotTDuZ35p6V52XvF2SeYuf0/7Qbrp/if7Hv
/wEVAzZe
"], CompressedData["
1:eJxdnUkOLbtxRL8BQwPvwjtgl0lyCQI88hI0MOCRB/K+vEVHsG5FsJ5+g3d+
3WKxzY5J6t//8T//+V//8tdff/3zX/Gv//jvf/7vH/R/f7vo7/+GP/Ree4wd
YwhXXXM34c46135xtD1jpnBFm2UYUdLUu1FG1qEfxwDUKYy2SxFmZG8Zxj32
XsKV+LVKzp09ZnkRVeitGPtCrfXjOWovaxlz9qEPoTnjqvOcWdrqL67S0Bl6
ujoa5L5ao9bhD62JDujGHXVXdd0uM3p5S0Z1I0ZMITo6+1tyq6WOrX4Gtu7v
NnR0or+E+GpZ9cVW0Yq4sJUR25gleggbajLmhat2VRIDstwbbawV3e9G6bHr
EuI7I1TJGCVKVmPk0LxqmQO/19NEyWOoqJm7jqnvojlz1TRuVMxPNx5qbrQ1
MVVcZwzCrO3FjhnXyn6b0GvZDZNF2ApmtLBhjKZ/jAmO5i7hwkRqwmgYQo1v
j1V3qFY9WywMkpAN7m+394klmEM/nii3jWKMeX13FUymvoUYhJjTiDmbxllr
WSqZ6zM0c0bZG0v8HQVMZUwy9TOWzV6tdmEmuks/bpjPU9UYmIWY/U2Ibt/L
T5PSwE/Rwq1uh1BBNadK7gVzdk1hw0+HqsFqYvobMbeMqPScWt2Dg1+GqhGY
3qsVIQdNKwWrEWLCTUjIqCoBNWbpq7nk2XNvjT6aXu9KUj6FllVgxY2l5Yxl
ETM0oEHx1DSfA01Hzd46B8dwqGQIUfyHOoS9ZBaVPCDc1oWYVV2T8OBYLgqL
e6YwILIgZ4X40tBix6SJ5bUQWUppkipAvFn9tEEEaUAjZ47rQ6giJJqawI6F
OBC2FVViE7ibhRt0D553dd2ixNp6F4OLeaZqYN5gUb7vYnFSq7yDAg0BsSjJ
n5g4G/97EVKUaufC7CuMmL+S3ok6YDnrxxiTihYKNySWZDvWOVahxhcDhJUT
qgbqtLffHatQkRhRJw1KQgIPT9HEiIbHNzlG4adZ0Hgt9sSgoA3GhbkvuZGz
YFG5gVCpa0qK5hyYklpWKAlrpadwLehFVXJxyjb9GJp8DheFKde61ARrAdGg
voJiGxCFRmgGTW9YARk11O2bM0VDNkvpEH5NmDRV3o6d0Mdo/VuNefSrJj8Q
Ez6bEYWrVrOh/lXNn1CEkEjViCUYeeMs+0YrzQevD0HftH0/3RkhhPWBZWkc
aWmGbsOicov6piTVjwdmwtCygsJp05p9cjFMrTJiWCLBJoIglH1FAYOJZGyJ
5qtz1pkPzYjpK1U+NxYGhtAIc1NWH9oO0a+1gLbTvnp7g3otYO0IMZ2H3l21
Tf5biMlStXAwx6DqVCuI2wVRoh/TsK1ST8DkqjOiq/0h9AdspnpjlVlL5GR5
kbNqStMRNxTjjU0KCAjVsPuNNj4hJDC8w09pMN1PUefiD2HxYp0ZaVKokhi+
YQGFuds4akZIA1lBWFGYSm4g+mI3LatFUTCNG38PyRz8GUae5gbdA+iz98cb
IpZGv5A2keYkFCodkbevYPJBFWjIMLlXsbW5oScxKs24YIJMIVZ/0TpCBSt6
oxshNyQJN2wIjKhqhRpD8hvRkzmNsAmwWIQw2rdkLAxAaBXXCsMJW1s/DtiI
eOHFRINtjEEoYM25CUmhkxfCfdIafHD4XVgUtkaAG5pc36XB0KeLomKT7b25
eJdWCmzrRq/mxYWeWu4NTnf7GlCC6HYPKJ02m4ibVer3U85Rl3x8AP2YJv7S
BIYmp33hpzQuPVUgyatFEBCCT8Y28ZIqwEwrevwJFvGru0fhItqvuCai4Nfc
IkJP5P7ga0IAYbqMV0ABqc/eJQkcGP13yAb9v3m/e3So3qWN218JDBz4Z6oo
OM9TigDTF0MkdxjYMc+KSoaDBKk6X4QRAUmhFuEv2hFCiNEdyzhrTLUXtkpZ
sxohj91XA2Pf3QRIpCqXBwhLXLYKEU+vH0OYYxCNG4JCP45S7HkBG9eOGggz
vmZVNZIef1GLoLsghdI4PIGBNBOW34US7KHvToqYZqzQwK+V+6LehdDA+8OI
VempAoO/tOtpQhZuVQN9Pq9aQau3sfUuDOItBUSkm76M+A+uM23pPlzUoq2u
d2kCtqVq7HU8zx9Wzn65w8BKy89PYTPWVzIM+JWYpGGklaeepAFoy3zQeh7S
ZUBq71ezAzcXqH8Mszz8ocbR1dyApQKp8yovCl9I7+6n8DtKVzVQQ9jXfgrt
219pRoT9mBfSsFet4IrFcDXgMKG/yoXQqHoXK3vLLwMufEgrBU5JvWtFTV5f
CQxcWP5DT6noSitGimFVI6FkinsD69PuEjUXPVE/hWVTQk+prNJjBMWewz25
IBy8nOkMFkVdYDqiIuFaUcVeRWEWYVzep1D6+5p1rdA40URqZTIc9nYdlw2k
gd7l8EtLAukuvLYZEK+O9LtczeF39+m9F9uxQFQUPG9qXSOMfA1Zo2CUCwDE
mrw+BJmE2aKnp16ase2YdZLtcAjgAWnyYxYxNrSMY1lNwBTFELrrzmrWGmwJ
eRtVzYexDPtCRS2Ginoa15aLh/rCKy8SBXCkOyW4EH/LA2IMBkbeDiM9vneK
diqzphH84TJC0Ozr6SpWQESs0reBjN4WLw1GJCkNjbDVXucRyPiNxggChr6L
3mU0dy39mGb/eqOXgyGcqRjF+PlA+jH9yrqnMRk5FGKRza06Qww0CyjYnpUB
TSHEiAUFZ1mVkU+EHtDMgVDBstHo01DtU1K00zRby3j8Fn0o+XO36OC+MKEL
1Pxk+HVqjPAMXWmEA1hDLYI5ARmjSsKoK10SqZ+Iq9YgVgYG0KO/WEuP4GKs
s/npjHl17Fo0IvVdiDJ8txlhB3oiYTXDflHJmMDskR/CZoLY1Jw8ppscIiIE
zevvj2O7WB9R42Lq+Me0Ef1jyOpis4dKJeXCM8QI5VxvjJBOgTSH7+VqPDiF
iUqpn4H4x7XCdKbX+iKEXVQNKIXOtCigpEivssG9iz6M6KmhCfzDfiHVhhHt
d3upZWwxjrOyyoXwiGSNDMZ7crrkXLQhPrhdq9WLAgs/TFdjY954fB8cX9R3
B7eu3M8YzCI37UVVg9tUXcINDeD2RH7QY/Sg3+X2gjsn1tq2n3+oojC8dYYR
imxItcFzQGvdk7MwStqMq8sxAUIdX9OMBa3rKTWMbFEYz5O7MR+UXQfFjPkr
Uf9DVXLBbrnmBgR/S09RCCsYm+uDnldwNGCrjA9KAlOGVgVvX1R7N7piyEj4
oZqw27rUBGxlenHji29PwrwadBeFPVKRT0ZR4NOlsFKbq4EBgwPu7xAOaFHp
lB/qXW5kDAnVQFdMz9gf6ikkTig4QIS1oc6Bf1MYsPygjLHo9AciPph+SnfJ
333MwPlFlcwtn/C7D76jEJzqNgL5Q3pmX1xGWhjji6ok1kLR3jEQC1a7wy/q
x9B0MJjnB6UWYZTn3LK+fugfw5msEtfcWJz2+H7odxNq73p6wh37g3H9eE7t
tL6oH0Ptw2ioxt1sUfxQ8wr2FJbojZej/UN9FwYh3MP1weUPoQ67/IHqZ/Q6
1Ex80d+lybjrF/0ulvPu64v7QugNdTtWaDpGAcTSkswJvJrW7NCIHAX/GHWa
oxsjbWA8GNeP92Uy/dDVgDvYxh+oJmxu/1/VOPh2TpaTDFBurBIFNL5ayi97
UILxh0uIBelB+WET7tuZerD6uzTTNdzoVG76tS8OYzRPb9h0cI/W+KIaCHMa
/lAxUsmqgY2+4voDVY2WTKtQi2D1RPeHYPAzZcOI1S8dCuQYqr0M9HnyJzc9
p8boQRm9eezt8LvwhmrmF/1u0lRXJRncVT4DkaGl/sVxIQzz/sX73Xa3iNju
H6dt0Qf7VQ30RqwvXj/GV9u68ZpmgyaRHPwf+umZ3aoGfVztDg9u7zrH5sVl
bIw5flAiKOkE7OXvjkJf64th5PL+A10NKp0aX3Q1GCZs9YPXh4L+/vii3+UE
97J60C1CL8fVdYyge24wLDi8YBmQcpDth9fTvS2QH/RE4kIoXpIPuqjByaBq
QNWVvD500B+iGvQqg9kC82V/0H2FBjCf5YMyIZgxdAs3TJ1eLJGSCtbz+UHN
K0Zz2vyil8aD44v+0GLw7w9UA9G64iBqcjMlFZ3OSUHqroPzQKtRyDjvmF9U
yatE2ONL7j4UGQnAE7P4oipJlWrn8YcuapUdlkgP6uk+Edv+xe9T6X0ghOG4
frzQkUYuK3+I+0UOd8zCibKM6LqQ9J4UDBHxxSmMymSnD8o/4gZYV7rdi0sI
lyA1vX+o71bay5pmszLnQLP9hyoK9jFj0l/MC9Ma58F9Pd0wg/1ucgthG5km
076YX5wflJAhhrUzN3DpFXyxGvG3pDd0AGTu9WPuVLrOjSur+elkHLV98R39
2alCZMcS0/YznSGYDPNG5ckAGWYdfkoTUf7gwe7vwsupNnp/qKIgcGaTSv2h
imL8MTw3gr62a/Wgn8JGXv5u0PvXwoHoQsfKewIyXn89PUHYC7s2Ig/Ckbsx
HbEheneYiOXar6eTMQ4jN1/KhXlN/qRPeP2YiSIZH5yuMx1L6X1iOk7IMBFc
UbcXv6xXUdz1mddTmHG93DivWk1uTPtDTOeQvILc4+7bF+XTUUNeW41z9sJp
eCGzJW5ULsTgdu7dfIx3uyQSxJ63Vol7KJvlh67zKsyYUzXWOAJbCBG0ZXvD
vy3cQxLCgrLfzb7YjkA+OC+keWmExXgtdiryVG9gVVTG774Ywrprl/mxmLm3
1e1oENwcjT7neleuC4PCsPu2ET6LPRHiUlbJYJp1VcIzcFcIRmFjjqC0BvPl
aG4Lobgtclfrs3s/dMFQ5760kIaenNbFXIgpRXBGZEvUQ2cG3FCVzLhuuxEV
k/e0OCG9w8u0PWav3ZiyRphXi2mod6G64LhdiMGWDl3w4dPz+eDWZCBuxzaZ
yYPJo66L09PCPA6GKsntYJtbTHisFvWLuy3Xjxk0dDTgpL7YS11cKkXhO4aJ
ml34xbminCIg96o8GR4M41HYFy7H+mgQ1WsUDrr5MKC4sWPczVu66NWEreqS
N9zw4pJhnYTHCD0zt7t9cx9AccLFVbZlEi/MhbR5ybSQ2MtF4ee7+8f4briS
e3PxXE9PMtMPsWZgfkgyADFq0rCwpZln4adQyFW1Ypb99q7lhqQLB6uB8xJB
m1kFLfwU1pi9J6YnUWALO7pOcWAgJppEEFZvoeHwYouzef7FZYReHNfTkxcn
XMzzVMmwyukWvAizLR1ExRCN4hjUZnRzDCPzJTWvHpQigLWIOay1wISEefXk
g+PCFS4qmNSsSQiJy47Vd2FoN8vnDfu/KasTxRamYbQvhrENbxeeQLa37OEb
MvFCvcEAuo0xngTIq4GLcQZJ701dlW9gIQr6jYaBkKLtFTJEyLvup/McHLlw
5yuBubu/mZgrXOF9HHp3qLM/BOe3a7flQQUV6fuVKhcPCAtybtWqnVMnxqAU
uRDiKl3Uor+sStLdHcbOBLupd5nxqqQ4IlbG69HTDoP6mUboRB3fwLpmQkbR
u1jKoSw4zJMyQrE+IISGtAawMcVbgwJB0JTQDsSAamsmCgNn7XVqgOjHyHXj
dOfAoenhEUxGw9xA+v9tppFK1niUpt+dPJ+kd5laeU0GOENVJ1CCIfCdbhHt
/3CtFt2lCOMJ7gthbUrWEc+G94XewiYyO3HdmFvdDskfs7oaC+aVp+iitTLr
jWN8cI9yIabHjcwfvhC297gwtSt9cNZ+f5fjfeGWfUXErLq/27yNdZApVhdC
OFxPj59mHKGtVSIjK3HjvrqdSa/lepcz9KokW3h99zJrD/Kg2I1KyQgmljIx
19icwk3kHrc7h2HDvN7liZvr3XSaLpE5gMJNHzaqcVblq9C5xSC4N6D3xizX
012vEWTUvzf1FRNOluXV2Sl3AxlzuMQXVOisnhsQ0EOn7Q7GShcFM3+sZeSR
KZe8sQYtzWDGd+2WMiEdjX9FfdA+ZnaBEEbP0gplINORXiBP5kk+VwodCwpu
US7t/xLD2SzADRWqiYQ1hX50NYBMKhIyr0TtrYxGhmvFM5DlVV7EaW8CSFN0
6Mc8x6fsDiAzd1c1wqFofsrIgaR3PRlIkpNwOyBjtPYrc8S6pkqlYa6DA0DM
Iq+FykzV0ErBrKmMdF/o3TSaIsFEE+Psw/0c9JWbEZ7jbPoud+10XhII90Hp
skEJU7WBAtw85FiMUBruHB4u07m24JHPvMZo0or1gMILWdpOAtKw0equ81i5
Kor7nV0yh5bInB5QmNO0XIWNrppx0JLVzNk8JOW5QdtF+TmYJliUiiLy5CRk
kL7LyA9P+xgXUw+EJ180jKMrZY4TsPpYwQk4wanVU0xoZwwSmSwyjftav42n
U1LNbzBri/bpGGzmudUL8WnNDVRw+BQnkdvlagImAlSuagXTJXW+LBifC52W
DabJp7JKeCxzUFIa0VMyThpzq61xGhODFDgKpktWG1S0eZxsSTx5r0Im5EjG
thNZCRcFC8qLjg4B7JxpzHr1BnPGxvWU8iz9FDNLcf6DWTy+cY6OaFCC8XdJ
Bp60XTbGGs9QyR8MmjXc9RXGyY4wojcu3OjHIjyKXbZoY6Qg3ZOYzuElCYRD
6Im0kjuGLorH3LQW2qYQkqBgHuOwlmzwELYiGBDjjfGPJuQ2taz6Tv2kMxeY
YhRmGpSzYa88VeCJDC8hFHk24Zmj6ismgUEPpJGTIYRwpEOzrqN3mDkhhE5N
f6iz45Zx03ZTyYPDK5uQ9mbRDm+cBa1zXsGjmN0uADEV6IZsppTtqmTyLHjz
U2Z8aj4z2zC0Vx6sIF3xFyeV8TJyu0jaitmC2+sXFu1gHqBxLdsqMOlrVd5X
ULE55ZXI8yzGBt/R392NB61VMkY7tkcBK4xH+X7IJKDQdnCcdP8tg4puJmOO
Rsa/3s45cewto4gY1rDMDk9tzNFK4+HhNMIo0ggyD5uxtBcbIxSShIP+nw1X
ZjG27koyxchezMlx1HUNxOlUecbHC3OQbtSmPJBjNI1MD3admQ3Swk+Tss9P
MTkUYo2TE9i667wZk1GLmLLhJcm0sKrktOD279LxWOiTyiCF+ioxrZrs53FO
QEqlcoNgNkmVweSd6gZS9A3JDQbcplXbmLxGwqPAM5B9Gmdsu8OMdC/lA3P+
oZ81J6HlmdZp5JHWZuT+vdYC7ZhSJfnHPrJBTYDuyvBk2DxzLosiuIen6zhO
RKb4xzR0urLfKcmZ3m5kdqwMdWBuRYmBg1n2KpmzWzc/UJDDrbl+vHhe4e0N
ipVmOzaojkOyjgj3WUVhtU8dGYs4CcGShA/K+HwWQ9WHmNWrs9LBAFWzccLe
qUoABkKaFVeS+Z8ljLmc6wJc54Sh8eQjvniyeWSaQilCingUuIWvffbA8JQI
N5BXW4SEaszJsPE7CZnpUrUZwfOB1fv7wGS2WjOusDoOLhMFu4CbWY9q/j5J
3RqyzdCXFg5k5GS61g+ZVry69GBSeDXZDFQZ2/YVmzcU6KavQMn3dk4yjrBl
bZ7UJp3lYc8tn+AOHjwtSgaIc5BrakCB3Do20g/T9M5z4kR2DlTZXEqI5YUE
9RqjpE7V4Y5gCuDUTuuDOntI3F2bepFo7NQ+Dm9UYC6tmn8y7DQ3kiOiqx4w
NVANyxxeA5E6ds1URLpWejqPilGdFy8oUCAFY88domacsdwb3Ke6eoNnGNeN
K5b7mRdO2G05qNRi7sKVrpO2RKYm6sfM2C+uxqYwc19t+uVuEU+oD+myZNDb
YdJz54vS7YjcylHnwDvs2g8l8u4OV6MzCcHvdn7WJQ+eZLrwZHgLaV5P1+rs
mPkpU3r1IYw1pobmFXQIjzwKa2FMYxghn7ToJq+UsLYiNjtiE/3GtNYXYZsw
Sf1FbtKGRN/sjBI3Y+MlC0aakMXvMhVVEngyWTSlJiaPMlU3cJywv94dDLpp
xs5z0Ym05DwhHBmBrGDVoSEgr98J/7ifJEghpXf6xyOugOSk+LYjxlua6JcL
Nzdu32U150lGq0Zm2ehdVLo4BsVN9+FwFnx75pUPI80R/ZiZTTqpd7AveV6T
gb9+vcsrg2Rg8CaEXtx16xzx1rubkXtPlc2zeJKx+AZeVT8vrLjhUCeqzIT3
cmHqVDLXTPEhC25SMZOxCRkk9rtMYNaVGrxPBUZvLxeiR6aQYVOJkcUDcY5R
LFRq6hhUMHDddKsPkFlzxU9RTZtqiy6Pzkw9B1rttHLveC9X8uTZKxa0aObr
cEeso541ryAXB023F+Fzc9tWSAm9/JQ7wK4kU6x0cpzIzdIlhAeok7bE4XR3
IkP13cjsFVWSR3Ws6BljajqZyHPvVLp+F191dBoLMnxKFzhrWhJyD7cowyqo
bNMRZmgyHlb0jxnO9Xf3k30oXAy5vi3aPKOuE77ENXQrSHCbMeJGuLQSBUBu
03YhFqESgIGbNyCpZJ6dtO/MAHnVYSUg/H1de0I1x5vX0kjbTEU1JlS1C2HX
diOPabuSjZmcGt9NDz/lszMz7QrCbG496RIYIK2X6afJoxGq1bN9NozQX5Ib
PAldHdnePFCY4aeLUeMLc1mYY4CqD4PDrGMClpt/0F3HxaArU3gqgNv7qiTz
BsIfgrQKh99pIfK6rQdpajFgO4Rn72UaV+g4IXAc01bIY2y1f9FFwZBdXUVV
RpTfWQc8Xlr/ot5ltruMhOSBe88NIpy0pXfhDkC+qeT+HL8z7qEcyBeXkHbg
1od4n1CrRm7jvVOFaU7Q1dePacZ9URdAJZ0y3/h0bG1IPn13MFNoG7Fgs6j5
g8FLt/dB9SQdHAnzF9eF8E1VK6b5levH53qG6+nyfsqLLopWj6sRvNtu+l3O
B48glg3dxQt7d4uy0mmvX2zG7SzWH7qSDH1J8r/o7zZeJeXv8so999XBN6x0
DuU6K+zFfeGQP5jcWYaicyWZ5lkvhNWwjeu6gJEItepV9qC/Cz97XbXi+YVQ
NSZjP15WNHsUZwDC4NgesgdV8uLBvWqEXTM9Jx/sF3LfR9h4sv7CmZdkYNJY
dwN5L0/zgl0RvmznRf+YMYnUCC7m71yV5NajP7S5Izr7F1XUrgwFx43pFXpy
/oqR0RAP6IN+t1MrqtshRptHn8ndTFB6EdZXV5g0z10WMj55zRbvkUsjsyuv
p1g3q1zIowQX8hinMX2l5IuqBi/EsbwiTpm1RB6y6h/U6LPjimIyP6yqBlzj
lFsKpFWr9fvDMPLUdX6wu1bBE/kumTeq9Piiq8EUhaUm0GCQI/ZDzQ3uS/Z0
X3GnRsdGXtSHGPvTmYuD9nDpRzNjXdWgPdE8Rg/qQ+e6Rs3YB91XDFpc3+W1
PNVNONj6jaNcyKwhNRBmAD7sp/A8rI55DcjcLYy8IUfv8jrGPS6EI3Ih8+CK
hmwxjOIRZBKCsiyO/IVJoqcwKbpiBcwF5/GdJuStVRp9ZrymIp+JhTKXrsXg
cXTuoA3hKj6eQ4T7r1o17p5O6e5Gya7Ldh4MiU3iUmSMYW1GXVVy5wW4khuN
do0nQzv3DmuK/lAl88CYhUxj1piSLV/Uh2iJlevpwespTTX1xm8LVBiM9JYv
qq94FloJOdwAKrX56YMqKplAK0HBSzFC5nSeqyt69dPNC6P+QBXFWIniOS/6
aTv3tby4eCmOx5eblHWp6+iI6PgV9wD2JWMf1Chwj6+nNA6zG3wUInnJadPN
tDzRyYDPFzW+vCqpWQ/+cF+YOu8Ms6We64a+OC9MZVa/qKL6c5+UEbpNY8Tj
ks1W7rnKVPtWL6pkCIlLHfezGRNqPq/S0gW5eeKm8mLyxNV0SUjSTAgdSAHC
HVCE6sUw8mqA6ymPlecHm5Eekovipp7isYxxzyEH/0VVA2Zr09bbDyUo+jq5
PS6KuRMe/cV7ELuqgWkWFqrnklMbrg9eJTPIuPLC7snfuQWy3c/oi3lVktdr
XIPyoIo6x58zvuink8cI/HTPqnjOi++PeaFbtxIhhm6rIDJY4qfndp23ZF57
MnV8g8iDIE1YGSzoX5xCCKTt7x5sfvdc092/qFrVR24ac+rYV9KDq9ocf9FP
N/Nz9C4HW6l6PCwL5bb9dFCHGCfjdSq5nQFVyZAjWdyx59Indw434q+SOwOW
xT/evARF1eAgaB+WZ2d5btVPqThS3x08+51+us7B4xeZbafrsHiJ+jmoLRww
W7N9Uf3MlCqdT3lRo4/FHDqcxY3V1W2LMmZYtff0or474e/ooo9zOwNquYy8
NmN+USU/uR7xRfXk4iFtN+FBFbVQCzc/ysnO28LkMUdhfa53/2IXnotti5CW
ePGPadZpST44+4VdgdAHh5YGcdTPu7zmyshbvVzJc13J9S5vAKpCJmlLFHDr
rHjyw0DgPp+bwENv07Xi1VE7LkwLRuauDfsazCJZDg4QfcvNyZzmyd0XmaY5
3aIHVSuOWXdfce9Re0B5djFTwYE4Mdfdb7RvFUwcsD7itmWxo82rSrpCrC+q
zrS1rzofXHHhuprP7G+lUvOIH/+fAzRGqHHR0a0XVfJ8vFghQ1oyPnllfrfY
/OG6cHgNcn8lovrpk+7wIrel0iVzQ3N45iyes5fMCd6B68X+Q73L62SutcD0
daWuMYNmhq4RoFmKH6z5/8V23U0=
"], 1, {"Continuous", 1}, {
"Discrete", 1}, 1, {
ValueDimensions -> 1, DateFunction -> Automatic,
ResamplingMethod -> {"Interpolation", InterpolationOrder -> 1},
DataPaclets`EarthquakeDataDump`DuplicateProcessingFunction -> (
DataPaclets`EarthquakeDataDump`cleancombine[#, Max]& )}}, True,
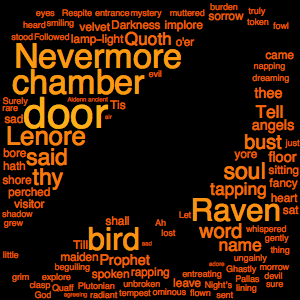
11.];DateListPlot을 사용하여 데이터를 살펴봅니다.
In[2]:=
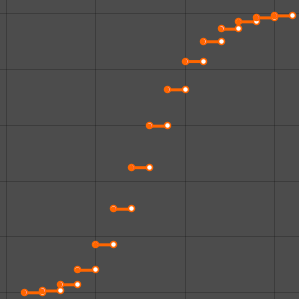
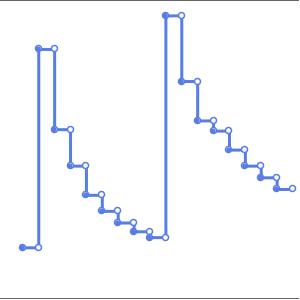
DateListPlot[ed, Filling -> 0, Joined -> False, ImageSize -> 400,
PlotTheme -> "Marketing"]Out[2]=
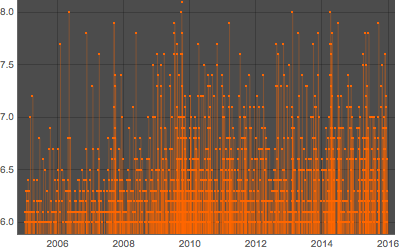
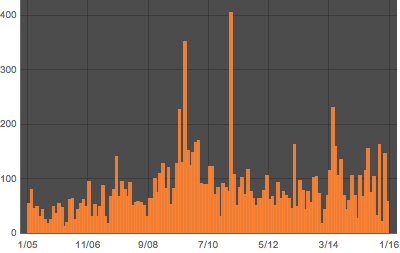
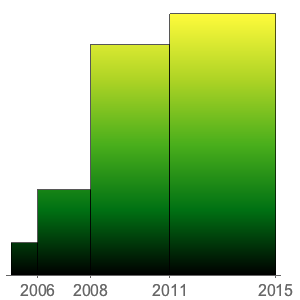
DateHistogram을 사용하여 빈의 두께를 1년으로하는 가중 지진의 히스토그램을 구합니다.
In[3]:=
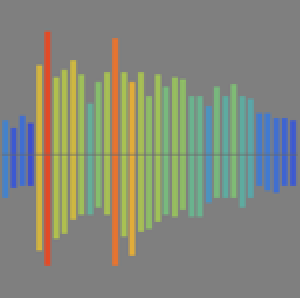
DateHistogram[ed, ImageSize -> 400, PlotTheme -> "Marketing"]Out[3]=
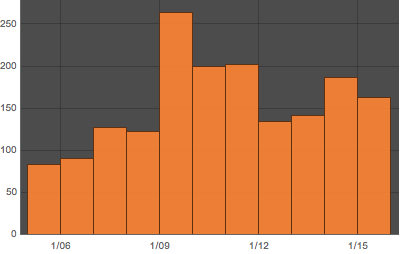
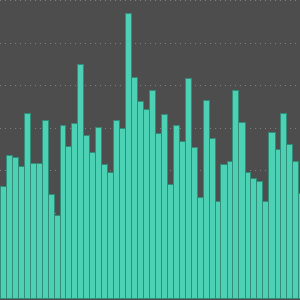
빈의 두께를 6개월 단위로 바꿉니다.
In[4]:=
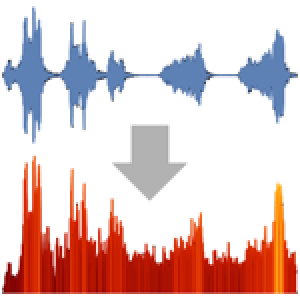
DateHistogram[ed, Quantity[6, "Months"], ImageSize -> 400,
PlotTheme -> "Marketing"]Out[4]=
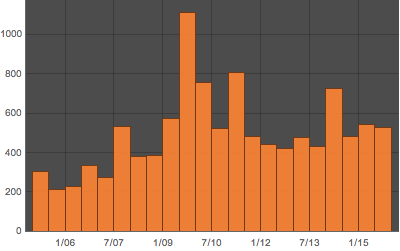
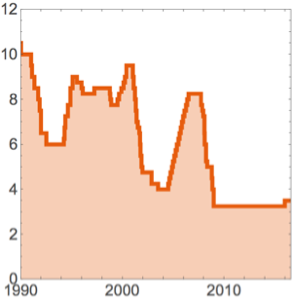
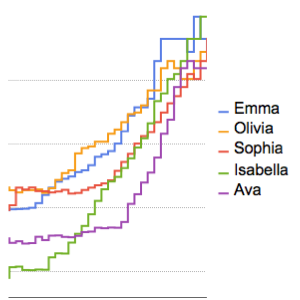
빈의 단위를 1개월로 바꿉니다.
In[5]:=
DateHistogram[ed, "Month", ImageSize -> 400, PlotTheme -> "Marketing"]Out[5]=