Wolfram Language™

Order Distribution from Distribution with Units

A system has three components, out of which one is primary and two are redundant. Each component has a lifetime following a WeibullDistribution, with shape parameter 2 and mean lifetime of 885 hours.

In[1]:=

{sol} = NSolve[ Mean[WeibullDistribution[2, b]] == Quantity[885, "Hours"], b]

Out[1]=

In[2]:=

\[ScriptD] = WeibullDistribution[2, b] /. sol

Out[2]=

The lifetime of this system can be described as the maximum lifetime of its components.

In[3]:=

\[ScriptCapitalD] = OrderDistribution[{\[ScriptD], 3}, 3]

Out[3]=

The mean lifetime of the system.

In[4]:=

Mean[\[ScriptCapitalD]]

Out[4]=

Compare with the computation using ReliabilityDistribution.

In[5]:=

Mean[ReliabilityDistribution[ comp1 \[Or] comp2 \[Or] comp3, {{comp1, \[ScriptD]}, {comp2, \[ScriptD]}, {comp3, \ \[ScriptD]}}]]

Out[5]=

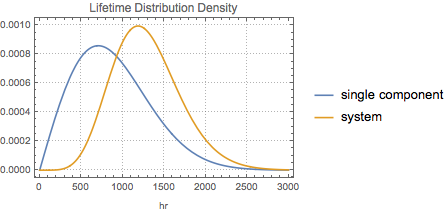
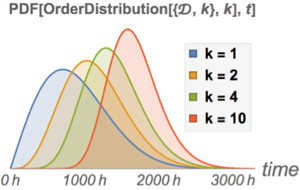
Compare probability density function of the lifetime of a single component with that of the system.

In[6]:=

Plot[{PDF[\[ScriptD], Quantity[x, "Hours"]], PDF[\[ScriptCapitalD], Quantity[x, "Hours"]]}, {x, 0, 3000}, FrameLabel -> {"hr"}, PlotTheme -> "Detailed", PlotLegends -> {"single component", "system"}, PlotLabel -> "Lifetime Distribution Density"]

Out[6]=