Ordonnez les répartitions à partir des lois avec unités

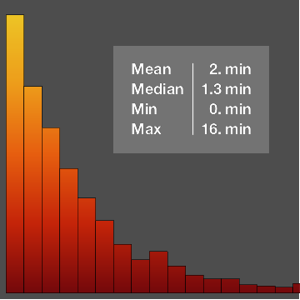
Un système comporte trois composantes, dont l'une est primaire et deux sont redondantes. La durée de vie de chaque composante suit une WeibullDistribution, avec un paramètre de forme 2 et une durée de vie moyenne de 885 heures.

In[1]:=

{sol} = NSolve[ Mean[WeibullDistribution[2, b]] == Quantity[885, "Hours"], b]

Out[1]=

In[2]:=

\[ScriptD] = WeibullDistribution[2, b] /. sol

Out[2]=

La durée de vie de ce système peut être décrit comme la durée de vie maximale de ses composantes.

In[3]:=

\[ScriptCapitalD] = OrderDistribution[{\[ScriptD], 3}, 3]

Out[3]=

La durée de vie moyenne du système.

In[4]:=

Mean[\[ScriptCapitalD]]

Out[4]=

Comparez avec le calcul en utilisant ReliabilityDistribution.

In[5]:=

Mean[ReliabilityDistribution[ comp1 \[Or] comp2 \[Or] comp3, {{comp1, \[ScriptD]}, {comp2, \[ScriptD]}, {comp3, \ \[ScriptD]}}]]

Out[5]=

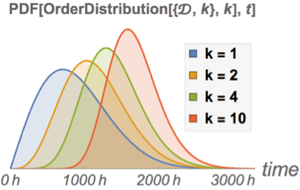
Comparez la fonction de densité de probabilité de la durée d'une seule pièce avec celle du système.

In[6]:=

Plot[{PDF[\[ScriptD], Quantity[x, "Hours"]], PDF[\[ScriptCapitalD], Quantity[x, "Hours"]]}, {x, 0, 3000}, FrameLabel -> {"hr"}, PlotTheme -> "Detailed", PlotLegends -> {"single component", "system"}, PlotLabel -> "Lifetime Distribution Density"]

Out[6]=