Verteilung einer Ordnungsstatistik aus einer Verteilung mit Einheiten

Ein System besitzt drei Komponenten, von denen eine primär ist und zwei reduntant sind. Jede Komponente hat eine Lebenszeit, die einer WeibullDistribution folgt, mit Gestaltparameter 2 und mittlerer Lebensdauer von 885 Stunden.

In[1]:=

{sol} = NSolve[ Mean[WeibullDistribution[2, b]] == Quantity[885, "Hours"], b]

Out[1]=

In[2]:=

\[ScriptD] = WeibullDistribution[2, b] /. sol

Out[2]=

Die Lebenszeit dieses Systems kann als die maximale Lebensdauer seiner Komponenten beschrieben werden.

In[3]:=

\[ScriptCapitalD] = OrderDistribution[{\[ScriptD], 3}, 3]

Out[3]=

Die mittlere Lebenszeit des Systems.

In[4]:=

Mean[\[ScriptCapitalD]]

Out[4]=

Vergleichen Sie diese mit der Berechnung mittels ReliabilityDistribution.

In[5]:=

Mean[ReliabilityDistribution[ comp1 \[Or] comp2 \[Or] comp3, {{comp1, \[ScriptD]}, {comp2, \[ScriptD]}, {comp3, \ \[ScriptD]}}]]

Out[5]=

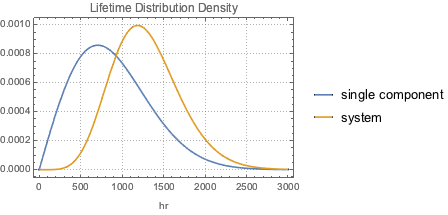
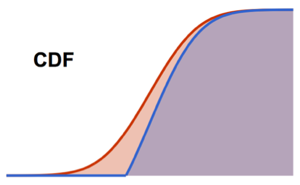
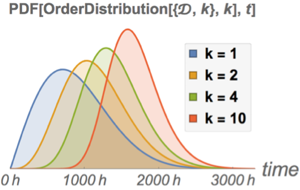
Vergleichen Sie die Wahrscheinlichkeitsdichtefunktion der Lebenszeit einer einzelnen Komponente mit jener des Systems.

In[6]:=

Plot[{PDF[\[ScriptD], Quantity[x, "Hours"]], PDF[\[ScriptCapitalD], Quantity[x, "Hours"]]}, {x, 0, 3000}, FrameLabel -> {"hr"}, PlotTheme -> "Detailed", PlotLegends -> {"single component", "system"}, PlotLabel -> "Lifetime Distribution Density"]

Out[6]=