単位付きの分布からの順序分布

あるシステムには3つのコンポーネントが含まれる．そのうちの1つが主要コンポーネントであり，2つは冗長コンポーネントである．それぞれのコンポーネントの寿命は，形状母数が2，平均寿命が885時間であるWeibullDistributionに従う．

In[1]:=

{sol} = NSolve[ Mean[WeibullDistribution[2, b]] == Quantity[885, "Hours"], b]

Out[1]=

In[2]:=

\[ScriptD] = WeibullDistribution[2, b] /. sol

Out[2]=

このシステムの寿命は，そのコンポーネントの最大寿命としてあらわすことができる．

In[3]:=

\[ScriptCapitalD] = OrderDistribution[{\[ScriptD], 3}, 3]

Out[3]=

システムの平均寿命．

In[4]:=

Mean[\[ScriptCapitalD]]

Out[4]=

ReliabilityDistributionを使った計算と比べる．

In[5]:=

Mean[ReliabilityDistribution[ comp1 \[Or] comp2 \[Or] comp3, {{comp1, \[ScriptD]}, {comp2, \[ScriptD]}, {comp3, \ \[ScriptD]}}]]

Out[5]=

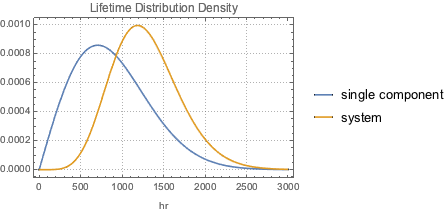
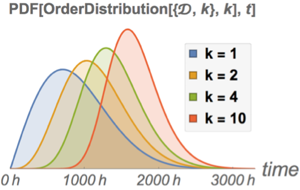
単一のコンポーネントの寿命の確率密度関数を，システムの寿命の確率密度関数と比べる．

In[6]:=

Plot[{PDF[\[ScriptD], Quantity[x, "Hours"]], PDF[\[ScriptCapitalD], Quantity[x, "Hours"]]}, {x, 0, 3000}, FrameLabel -> {"hr"}, PlotTheme -> "Detailed", PlotLegends -> {"single component", "system"}, PlotLabel -> "Lifetime Distribution Density"]

Out[6]=