Densidade espectral de uma matriz

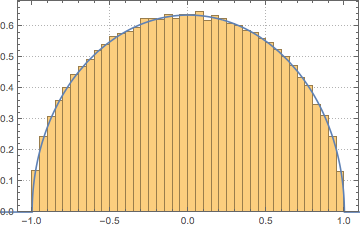
A densidade espectral conjunta de muitas distribuições de matriz tem uma forma correspondente universal de limite. Para as matrizes aleatórias hermitianas com entradas independentes, esta é a lei de semicírculo de Wigner.

Para os conjuntos de Gauss, a densidade espectral das matrizes tem uma forma fechada para a dimensão da matriz finita, relacionada com as funções próprias do oscilador harmônico quântico.

Use MatrixPropertyDistribution para representar o espectro escalado do conjunto unitário de Gauss e forneça a expressão de forma fechada de sua densidade espectral conjunta.

In[1]:=

scaledSpectrum\[ScriptCapitalD][n_] := MatrixPropertyDistribution[ Eigenvalues[\[Lambda]]/(2 Sqrt[n]), \[Lambda] \[Distributed] GaussianUnitaryMatrixDistribution[n]];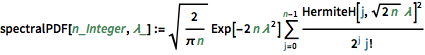

In[2]:=

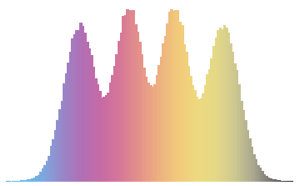
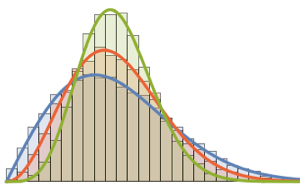
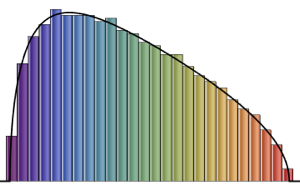
spectralPDF[n_Integer, \[Lambda]_] := Sqrt[2/(\[Pi] n)] Exp[-2 n \[Lambda]^2] \!\( \*UnderoverscriptBox[\(\[Sum]\), \(j = 0\), \(n - 1\)] \*FractionBox[ SuperscriptBox[\(HermiteH[j, \*SqrtBox[\(2\ n\)]\ \[Lambda]]\), \(2\)], \( \*SuperscriptBox[\(2\), \(j\)]\ \(j!\)\)]\)

Para a dimensão da matriz pequena, há um padrão oscilatório característico, cujo número de máximos de densidade é igual ao tamanho da matriz.

In[3]:=

scaledSpectra = Flatten[RandomVariate[scaledSpectrum\[ScriptCapitalD][#], 10^5]] & /@ {3, 4, 5};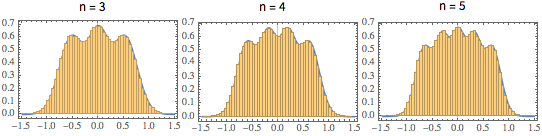

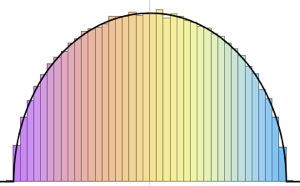
In[4]:=

Row@MapThread[ Show[Plot[spectralPDF[#1, x], {x, -1.5, 1.5}, PlotTheme -> "Scientific", PlotStyle -> ColorData[97, 1], PlotLegends -> Placed["n = " <> ToString@#1, Above]], Histogram[#2, {0.05}, PDF]] &, {{3, 4, 5}, scaledSpectra}]

Out[4]=

No limite da dimensão grande, a densidade converge WignerSemicircleDistribution.

In[5]:=

n = 250; scaledSpectrum = Flatten[RandomVariate[scaledSpectrum\[ScriptCapitalD][n], 10^2]];

In[6]:=

Show[Histogram[scaledSpectrum, {0.05}, PDF, PlotTheme -> "Detailed"], Plot[PDF[WignerSemicircleDistribution[1], x], {x, -1.5, 1.5}, Exclusions -> None, PlotTheme -> "Scientific", PlotLegends -> None, PlotStyle -> ColorData[97, 1]], ImageSize -> Medium]

Out[6]=