矩阵的谱密度: Wolfram语言 11 的新功能

矩阵的谱密度

许多矩阵分布的联合谱密度均有相应的普适极限形式. 对于具有独立项的埃尔米特随机矩阵而言，这是维格纳半圆法.

对于高斯系综，有限矩阵维度的矩阵的缩放谱密度具有解析形式，与量子谐振子的特征函数相关.

使用 MatrixPropertyDistribution 表示高斯酉系综的缩放谱，并提供其联合谱密度的解析表达式.

In[1]:=

scaledSpectrum\[ScriptCapitalD][n_] := 
  MatrixPropertyDistribution[
   Eigenvalues[\[Lambda]]/(2 Sqrt[n]), \[Lambda] \[Distributed] 
    GaussianUnitaryMatrixDistribution[n]];

In[2]:=

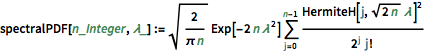
spectralPDF[n_Integer, \[Lambda]_] := 
 Sqrt[2/(\[Pi] n)] Exp[-2 n \[Lambda]^2] \!\(
\*UnderoverscriptBox[\(\[Sum]\), \(j = 0\), \(n - 1\)]
\*FractionBox[
SuperscriptBox[\(HermiteH[j, 
\*SqrtBox[\(2\ n\)]\ \[Lambda]]\), \(2\)], \(
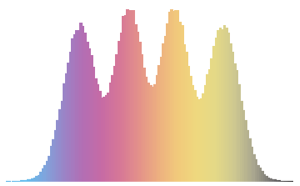
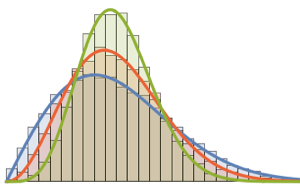
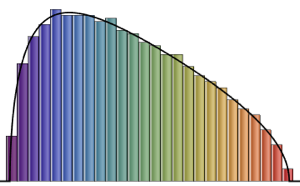
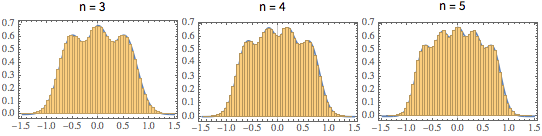
\*SuperscriptBox[\(2\), \(j\)]\ \(j!\)\)]\)

对于小的矩阵维度，有一个独特的振荡模式，其密度极大值的个数等于矩阵大小.

In[3]:=

scaledSpectra = 
  Flatten[RandomVariate[scaledSpectrum\[ScriptCapitalD][#], 
      10^5]] & /@ {3, 4, 5};

显示完整的 Wolfram 语言输入

In[4]:=

Row@MapThread[
  Show[Plot[spectralPDF[#1, x], {x, -1.5, 1.5}, 
     PlotTheme -> "Scientific", PlotStyle -> ColorData[97, 1], 
     PlotLegends -> Placed["n = " <> ToString@#1, Above]], 
    Histogram[#2, {0.05}, PDF]] &, {{3, 4, 5}, scaledSpectra}]

Out[4]=

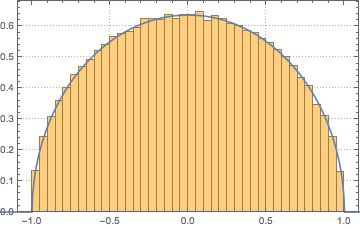
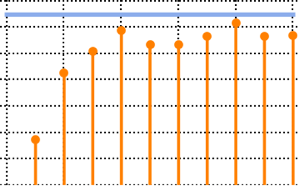
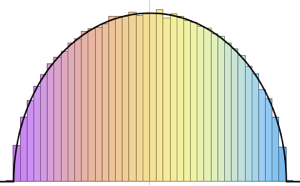
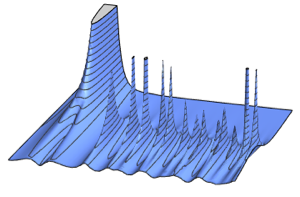
在大维度的极限情况下，密度收敛于 WignerSemicircleDistribution.

In[5]:=

n = 250;
scaledSpectrum = 
  Flatten[RandomVariate[scaledSpectrum\[ScriptCapitalD][n], 10^2]];

显示完整的 Wolfram 语言输入

In[6]:=

Show[Histogram[scaledSpectrum, {0.05}, PDF, PlotTheme -> "Detailed"],
 Plot[PDF[WignerSemicircleDistribution[1], x], {x, -1.5, 1.5}, 
  Exclusions -> None, PlotTheme -> "Scientific", PlotLegends -> None, 
  PlotStyle -> ColorData[97, 1]], ImageSize -> Medium]

Out[6]=

Wolfram 语言™

矩阵的谱密度

相关范例