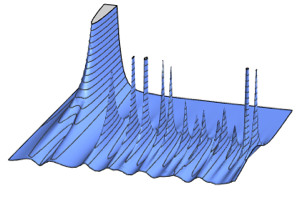
Densité spectrale d'une matrice

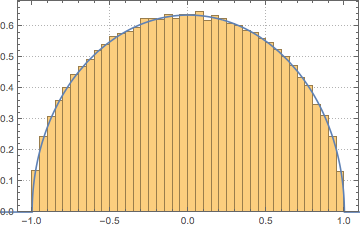
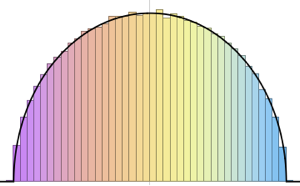
La densité spectrale commune de nombreuses distributions matricielles a une forme limite universelle correspondante. Pour les matrices aléatoires hermitiennes à entrées indépendantes, il s'agit de la loi du demi-cercle de Wigner.

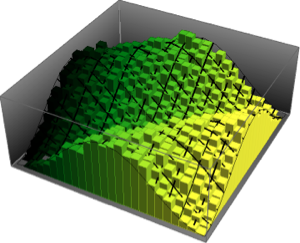
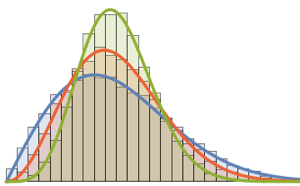
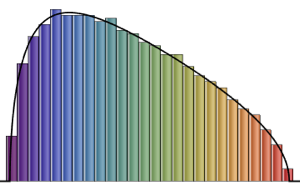
Pour les ensembles gaussiens, la densité spectrale échelonnée des matrices a une forme fermée pour une dimension de matrice finie, en relation avec les fonctions propres de l'oscillateur harmonique quantique.

Utilisez MatrixPropertyDistribution pour représenter le spectre échelonné de l'ensemble unitaire gaussien et fournir l'expression de la forme fermée de sa densité spectrale conjointe.

In[1]:=

scaledSpectrum\[ScriptCapitalD][n_] := MatrixPropertyDistribution[ Eigenvalues[\[Lambda]]/(2 Sqrt[n]), \[Lambda] \[Distributed] GaussianUnitaryMatrixDistribution[n]];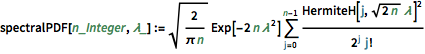

In[2]:=

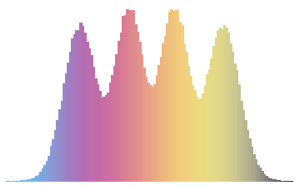
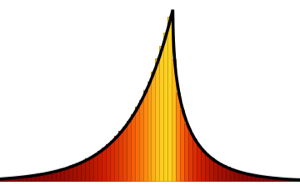
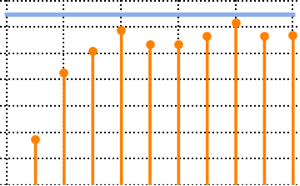
spectralPDF[n_Integer, \[Lambda]_] := Sqrt[2/(\[Pi] n)] Exp[-2 n \[Lambda]^2] \!\( \*UnderoverscriptBox[\(\[Sum]\), \(j = 0\), \(n - 1\)] \*FractionBox[ SuperscriptBox[\(HermiteH[j, \*SqrtBox[\(2\ n\)]\ \[Lambda]]\), \(2\)], \( \*SuperscriptBox[\(2\), \(j\)]\ \(j!\)\)]\)

Pour les matrices de petite dimension, il existe un modèle oscillatoire caractéristique, dont le nombre de maxima de densité est égal à la taille de la matrice.

In[3]:=

scaledSpectra = Flatten[RandomVariate[scaledSpectrum\[ScriptCapitalD][#], 10^5]] & /@ {3, 4, 5};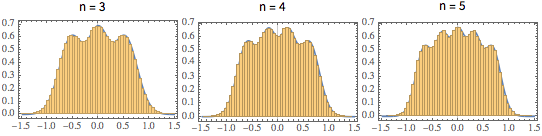

In[4]:=

Row@MapThread[ Show[Plot[spectralPDF[#1, x], {x, -1.5, 1.5}, PlotTheme -> "Scientific", PlotStyle -> ColorData[97, 1], PlotLegends -> Placed["n = " <> ToString@#1, Above]], Histogram[#2, {0.05}, PDF]] &, {{3, 4, 5}, scaledSpectra}]

Out[4]=

Dans la limite de grande dimension, la densité converge vers WignerSemicircleDistribution.

In[5]:=

n = 250; scaledSpectrum = Flatten[RandomVariate[scaledSpectrum\[ScriptCapitalD][n], 10^2]];

In[6]:=

Show[Histogram[scaledSpectrum, {0.05}, PDF, PlotTheme -> "Detailed"], Plot[PDF[WignerSemicircleDistribution[1], x], {x, -1.5, 1.5}, Exclusions -> None, PlotTheme -> "Scientific", PlotLegends -> None, PlotStyle -> ColorData[97, 1]], ImageSize -> Medium]

Out[6]=