Интегральное преобразование с помощью информационного объекта EntityStore

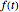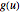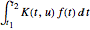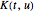Интегральное преобразование является математической операцией, которая отображает одну функцию по отношению к другой с помощью интеграла вида , где - это ядро интеграла. Интегральные преобразования чрезвычайно важны во многих областях, представляющих научный интерес, в том числе в обработке сигнала, медицинской визуализации и теории вероятностей. В данном примере, мы создадим информационный объект, entity store, содержащий свойства важных интегральных преобразований.

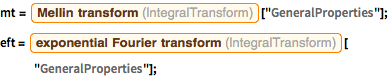
Информационный объект Entity Store может быть кодирован вручную, путем записи наиболее важных свойств интегральных преобразований в структуре данных с помощью функции EntityStore.

In[1]:=

EntityStore[<| "Types" -> <| "IntegralTransform" -> <| "Entities" -> <| "ExponentialFourierTransform" -> <| "Label" -> "exponential Fourier transform", "StandardName" -> "ExponentialFourierTransform", "StandardNotation" -> Hold[f[t]], "Definition" -> Inactive[FourierTransform][f[t], t, z] \!\(\* TagBox["==", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"=="]\) Inactive[Integrate][ E^(I t z) f[t], {t, -\[Infinity], \[Infinity]}]/Sqrt[ 2 \[Pi]], "GeneralProperties" -> <| "Linearity" -> {Inactive[FourierTransform][ a f[t] + b g[t], t, z] \!\(\* TagBox["==", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"=="]\) a Inactive[FourierTransform][f[t], t, z] + b Inactive[FourierTransform][g[t], t, z], Inactive[FourierTransform][f[t], t, z] \!\(\* TagBox["==", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"=="]\) Inactive[FourierTransform][f[-t] UnitStep[t], t, -z] + Inactive[FourierTransform][f[t] UnitStep[t], t, z]}, "Reflection" -> {Inactive[FourierTransform][f[-t], t, z] \!\(\* TagBox["==", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"=="]\) Inactive[FourierTransform][f[t], t, -z]}, "Dilation" -> {ConditionalExpression[ Inactive[FourierTransform][f[a t], t, z] \!\(\* TagBox["==", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"=="]\) Inactive[FourierTransform][f[t], t, z/a]/Abs[a], a \!\(\* TagBox["\[Element]", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"\[Element]"]\) Reals && a \!\(\* TagBox["!=", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"!="]\) 0]}, "Shifting or translation" -> {ConditionalExpression[ Inactive[FourierTransform][f[-a + t], t, z] \!\(\* TagBox["==", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"=="]\) E^(I a z) Inactive[FourierTransform][f[t], t, z], a \!\(\* TagBox["\[Element]", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"\[Element]"]\) Reals]}|>|>|>|>|>|>]

Out[1]=

Более полная версия интегральных преобразований может быть получена из следующего объекта облачной системы файлов, CloudObject.

In[2]:=

itstore = CloudGet[CloudObject[ "https://www.wolframcloud.com/objects/c21b356b-607a-406c-af91-\ 5088f435fe99"]]

Out[2]=

Зарегистрируем созданный объект информации.

In[3]:=

PrependTo[$EntityStores, itstore];

Рассмотрим его содержание.

In[4]:=

EntityValue["IntegralTransform", "Entities"]

Out[4]=

Добавим новое преобразование.

In[5]:=

Entity["IntegralTransform", "HilbertTransform"]["Label"] = "Hilbert transform"; Entity["IntegralTransform", "HilbertTransform"]["Definition"] = Inactive[HilbertTransform][f[t], t, x] \!\(\* TagBox["==", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"=="]\) 1/\[Pi] Inactive[Integrate][f[t]/( t - x), {t, -\[Infinity], \[Infinity]}, PrincipalValue -> True, Assumptions -> x \!\(\* TagBox["\[Element]", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"\[Element]"]\) Reals];

Запросим доступные свойства интегральных преобразований.

In[6]:=

EntityValue["IntegralTransform", "Properties"]

Out[6]=

Получим определения для экспоненциала преобразований Фурье и Меллина.

In[7]:=

EntityValue[ Entity["IntegralTransform", "LaplaceTransform"], "Definition"]

Out[7]=

In[8]:=

EntityValue[ Entity["IntegralTransform", "MellinTransform"], "Definition"]

Out[8]=

Сравним результат с выражениями, полученными с помощью встроенных функций.

In[9]:=

Activate[EntityValue[Entity["IntegralTransform", "LaplaceTransform"], "Definition"][[2]] /. f :> Function[t, ArcTan[t]]]

Out[9]=

In[10]:=

LaplaceTransform[ArcTan[t], t, z]

Out[10]=

Отобразим свойства Z-преобразования.

In[11]:=

Entity["IntegralTransform", "ZTransform"][ "GeneralProperties"]["Convolution"]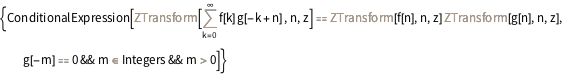

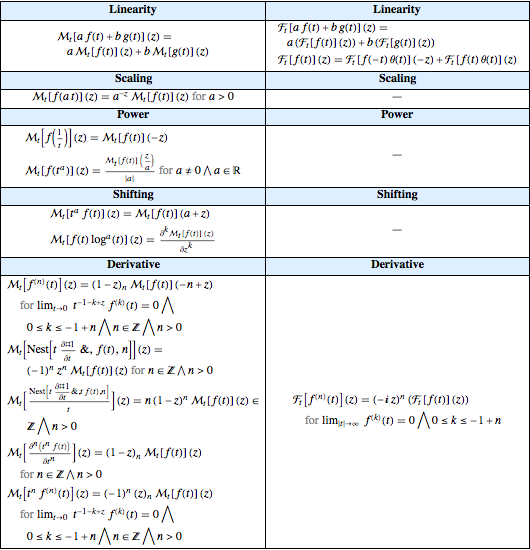
Out[11]=

Сравним ранее полученные свойства экспоненциала преобразований Фурье и Меллина.

In[12]:=

format[l_] := If[MatchQ[l, _Missing], "\[LongDash]", Activate[HoldForm @@ ({Column[l]} /. HoldPattern[ConditionalExpression[a_, b_]] :> Row[{a, Style[ " for ", Gray], b}])]]

In[13]:=

mt = Entity["IntegralTransform", "MellinTransform"][ "GeneralProperties"]; eft = Entity["IntegralTransform", "ExponentialFourierTransform"][ "GeneralProperties"];

In[14]:=

Grid[Take[ Flatten[{{Style[#, Bold], Style[#, Bold]}, {format@mt[#], format@eft[#]}} & /@ DeleteDuplicates[Join[Keys[mt], Keys[eft]]], 1], 10], Dividers -> All, Background -> {None, {{LightBlue, White}}}] // TraditionalForm

Out[14]//TraditionalForm=