Язык Wolfram Language™

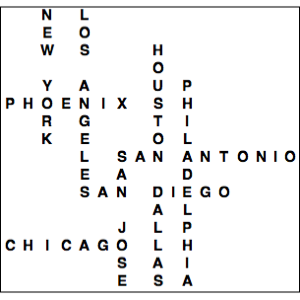
Оценить стоимость монет в денежном мешке

Мешок новых монет США украден из банка. Не открывая мешок, что можно сказать о денежной стоимости его содержания? Одним из очевидных и легко измеримых физических характеристик является вес мешка. Предполагая, что мешок монет весит один фунт, нововведение Wolfram Knowledgebase по валютам, а также встроенные способности решать линейные уравнения могут быть использованы для определения примерной стоимости украденных монет.

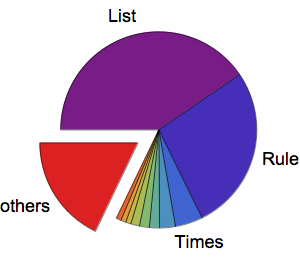
Для начала изучим список монет США в текущем обращении с помощью неявно определенного класса сущностей в Wolfram Knowledgebase.

In[1]:=

EntityClass["CurrencyDenomination", {EntityProperty[ "CurrencyDenomination", "IssuingCountry"] -> Entity["Country", "UnitedStates"], EntityProperty["CurrencyDenomination", "Format"] -> "coin"}]

Out[1]=

Разверните класс сущностей, нажав [+], чтобы найти его составляющие, а также отсортировать их по значению.

In[2]:=

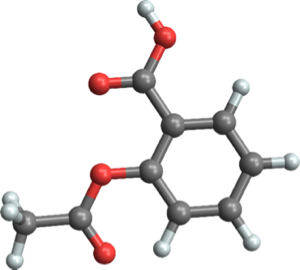
coinsUS = EntityList[ EntityClass[ "CurrencyDenomination", { EntityProperty[ "CurrencyDenomination", "IssuingCountry"] -> Entity[ "Country", "UnitedStates"], EntityProperty["CurrencyDenomination", "Format"] -> "coin"}]] // SortBy[#[EntityProperty["CurrencyDenomination", "Value"]] &]

Out[2]=

Теперь создадим коллаж из изображений монет.

In[3]:=

ImageCollage[ EntityValue[coinsUS, EntityProperty["CurrencyDenomination", "Image"]], Background -> White]

Out[3]=

Обобщим свойства монет в таблице.

In[4]:=

TextGrid[{ImageResize[#2, 60], #1, Row[Riffle[#3, Style[" | ", Gray]]]} & @@@ EntityValue[ coinsUS, {EntityProperty["CurrencyDenomination", "Entity"], EntityProperty["CurrencyDenomination", "Image"], EntityProperty["CurrencyDenomination", "PeopleOnCurrency"]}], Alignment -> {Left, Center}, Dividers -> All] // TraditionalForm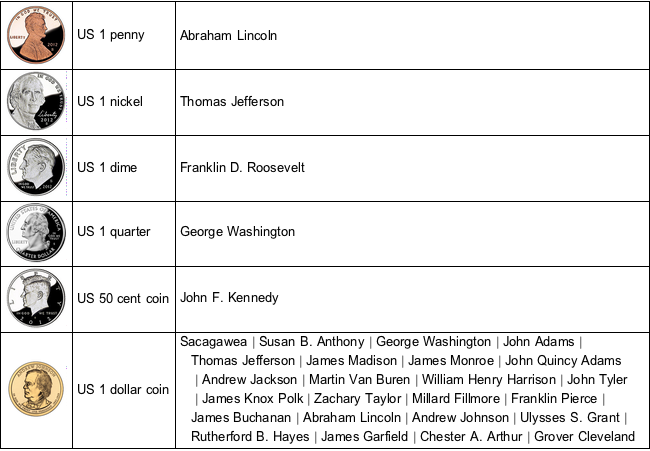

Out[4]//TraditionalForm=

Рассмотрим номиналы монет (в центах) и массы (в граммах) и преобразуем массы рациональные числа.

In[5]:=

{values, masses} = Transpose[EntityValue[coinsUS, {"Value", "Weight"}]]

Out[5]=

In[6]:=

coinsandweights = Transpose[{ QuantityMagnitude[UnitConvert[values, "USCents"]], Rationalize[QuantityMagnitude[N[UnitConvert[masses, "Grams"]]]] }]

Out[6]=

In[7]:=

lcm = LCM @@ Denominator[Rationalize[coinsandweights][[All, 2]]];

In[8]:=

rationalcoinweights = lcm #2 & @@@ Rationalize[coinsandweights]

Out[8]=

Найдем все распределения монет, которые сопоставимы с весом в однин фунт с допустимым пределом ошибки в ± 0,1% (предположим, что вес мешка не значителен).

In[9]:=

meanWeight = QuantityMagnitude[UnitConvert[Quantity[1, "Pounds"], "Grams"]];

In[10]:=

error = Normal[Quantity[0.1, "Percent"]];

In[11]:=

{minScaledWeight, maxScaledWeight} = {Floor[lcm meanWeight (1 - error/2)], Ceiling[lcm meanWeight (1 + error/2)]}

Out[11]=

Воспользуемся функцией FrobeniusSolve чтобы определить все возможные комбинации монет, дающие необходимый общий вес.

In[12]:=

allSolutions = Monitor[ Table[fb = FrobeniusSolve[rationalcoinweights, scaledweight], {scaledweight, minScaledWeight, maxScaledWeight}], Row[{NumberForm[ 100. (scaledweight - minScaledWeight)/(maxScaledWeight - minScaledWeight), {4, 1}, "NumberPadding" -> {" ", "0"}], "%: ", Length[fb], " solutions"}] ];

In[13]:=

Flatten[allSolutions, 1] // Length

Out[13]=

Найти минимальное, среднее, и максимальное значения общей денежной стоимости монет в сумке (предполагается, что все комбинации монет одинаково вероятны).

In[14]:=

coins = coinsandweights[[All, 1]];

In[15]:=

dollarValues = (coins.#/100.) & /@ Flatten[allSolutions, 1];

In[16]:=

TextGrid[With[{stats = {Min, Median, Mean, Max}}, Transpose[{stats, NumberForm[Quantity[#, "USDollars"], {\[Infinity], 2}] & /@ Through[stats[dollarValues]]}]], Alignment -> {{Left, Decimal}}, Dividers -> All, Background -> {Automatic, {{LightBlue, None}}}] // TraditionalForm

Out[16]//TraditionalForm=

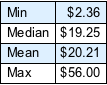
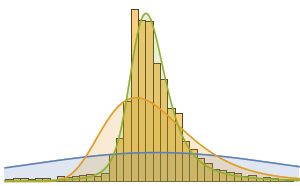
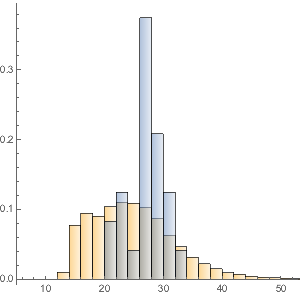
Создадим гистограмму распределения общей стоимости монет.

In[17]:=

Histogram[dollarValues, Automatic, "PDF", AxesLabel -> {Quantity[None, "USDollars"], "fraction"}]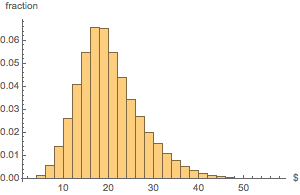

Out[17]=

Распределение веса довольно однородно.

In[18]:=

weights = coinsandweights[[All, -1]]; lbg = QuantityMagnitude[UnitConvert[Quantity[1, "Pounds"], "Grams"]]; weightvalues = (weights.#)/lbg & /@ Flatten[allSolutions, 1];

In[19]:=

Histogram[weightvalues, 50, "PDF", AxesLabel -> {Quantity[None, "USDollars"], "fraction"}]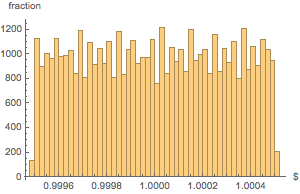

Out[19]=

Отобразим на графике распределение количества монет.

In[20]:=

Histogram[Total /@ Flatten[allSolutions, 1], {5}]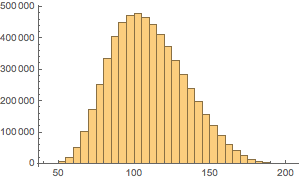

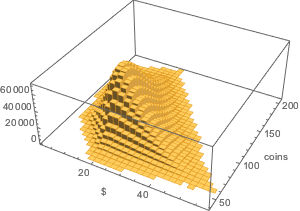
Out[20]=

Покажем бивариантное распределение денежной стоимости по отношению к количеству монет в мешке.

In[21]:=

Histogram3D[{coins.#/100., Total[#]} & /@ Flatten[allSolutions, 1], AxesLabel -> {Quantity[None, "USDollars"], "coins"}]

Out[21]=