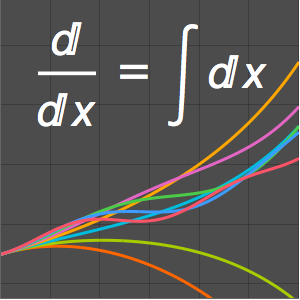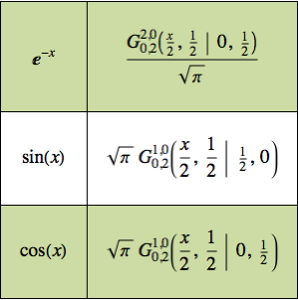Lösen Sie eine Fredholm-Integralgleichung
Lösen Sie mit DSolveValue eine Fredholm-Integralgleichung.
In[1]:=
eqn = y[x] == Sin[7 x] - x/a + \!\(
\*SubsuperscriptBox[\(\[Integral]\), \(0\),
FractionBox[\(\[Pi]\), \(2\)]]\(\(x\ y[t]\) \[DifferentialD]t\)\);In[2]:=
sol = DSolveValue[eqn, y[x], x]Out[2]=
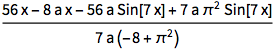
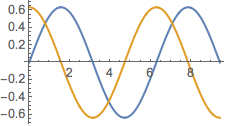
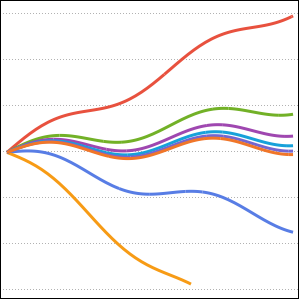
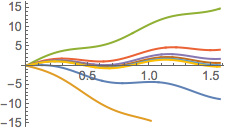
Plotten Sie die Lösung.
In[3]:=
Plot[Table[sol, {a, -1, 4, 0.7}] // Evaluate, {x, 0, Pi/2}]Out[3]=
Lösen Sie eine homogene Fredholm-Gleichung der zweiten Art.
In[4]:=
eqn = y[x] == \[Lambda] \!\(
\*SubsuperscriptBox[\(\[Integral]\), \(0\), \(\[Pi]\)]\(Cos[x + t] y[
t] \[DifferentialD]t\)\);In[5]:=
sol = DSolveValue[eqn, y[x], x]Out[5]=
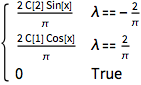
Plotten Sie die Lösung.
In[6]:=
Plot[Table[
sol /. {C[1] -> 1, C[2] -> 1}, {\[Lambda], {-2/Pi, 2/Pi}}] //
Evaluate, {x, 0, 3 \[Pi]}]Out[6]=