Wolfram Language™

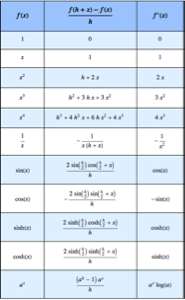
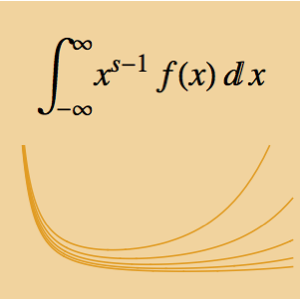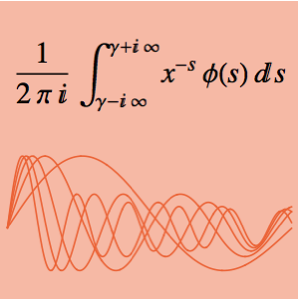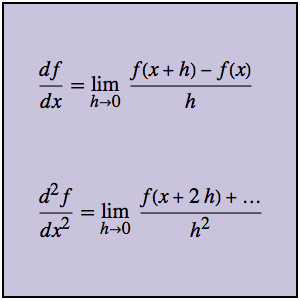Lösen Sie ein Problem der SIAM Challenge

Das Integral 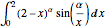ist abhängig vom Parameter α. Ermitteln Sie den Wert von α, der zwischen 0 und 5 liegt und maximieren Sie das Integral. Das gegebene Integral kann als Mellin-Faltungsprodukt zweier Funktionen verstanden werden.

In[1]:=

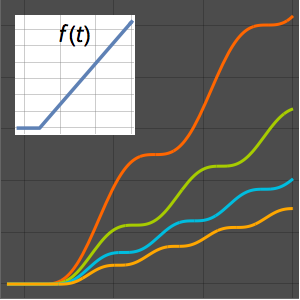
f[x_] := x (2 - x)^\[Alpha] UnitBox[(x - 1)/2]

In[2]:=

g[x_] := Sin[x]

Berechnen Sie die Mellin-Faltung von f[x] und g[x].

In[3]:=

(mc = MellinConvolve[f[x], g[x], x, \[Alpha]]) // TraditionalForm

Out[3]//TraditionalForm=

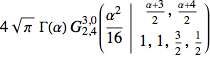
Vergleichen Sie mit dem durch Integrate erzielten Resultat.

In[4]:=

Integrate[(2 - x)^\[Alpha] Sin[\[Alpha]/x], {x, 0, 2}, Assumptions -> \[Alpha] > 0] // TraditionalForm

Out[4]//TraditionalForm=

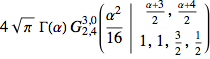
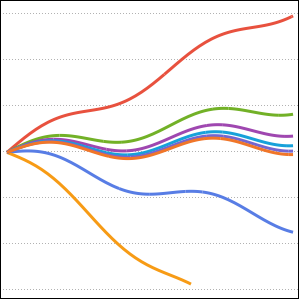
Plotten Sie das Integral als eine Funktion von α.

In[5]:=

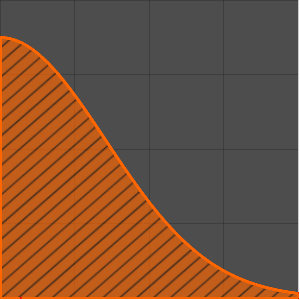
Plot[mc // Evaluate, {\[Alpha], 0, 4.99}, PlotStyle -> Red]

Out[5]=

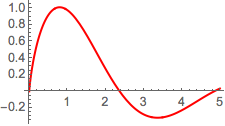
Berechnen Sie mit FindArgMax das Argument, das das Integral in 0≤α≤5 maximiert.

In[6]:=

N[FindArgMax[mc, {\[Alpha], 1}, WorkingPrecision -> 100][[1]], 20]

Out[6]=