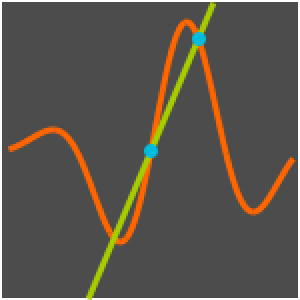
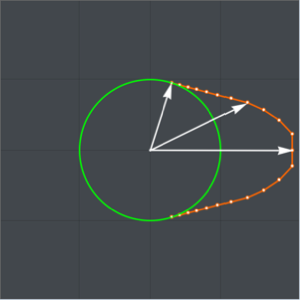
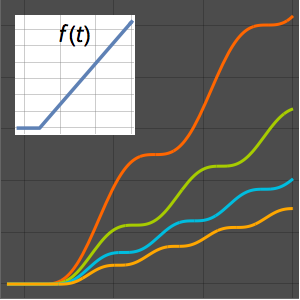
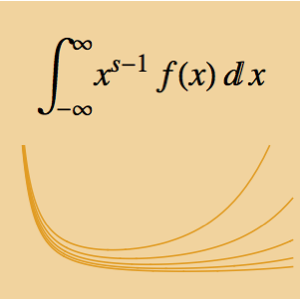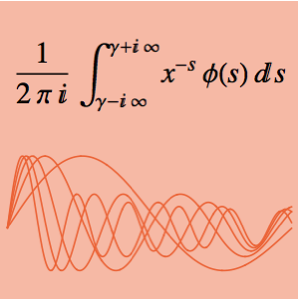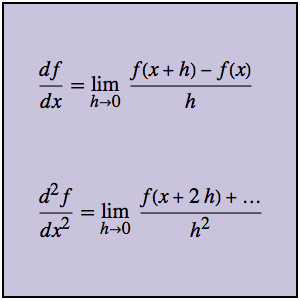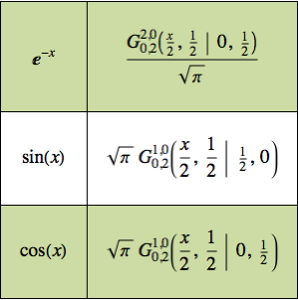Ermitteln Sie die Umkehrung der Mellin-Transformation

Berechnen Sie mit InverseMellinTransform eine inverse Mellin-Transformation.

In[1]:=

InverseMellinTransform[Gamma[s], s, x]

Out[1]=

Ermitteln Sie den Bereich, in dem InverseMellinTransform holomorph ist.

In[2]:=

InverseMellinTransform[Gamma[s], s, x, GenerateConditions -> True]

Out[2]=

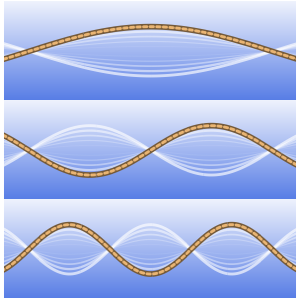
Berechnen Sie eine inverse Mellin-Transformation, die BesselJ ergibt.

In[3]:=

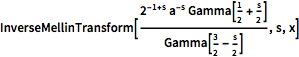
InverseMellinTransform[(2^(-1 + s) a^-s Gamma[1/2 + s/2])/ Gamma[3/2 - s/2], s, x]

Out[3]=

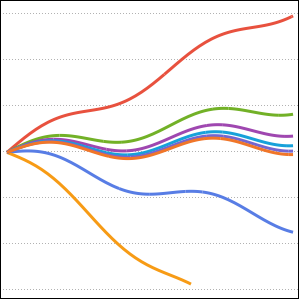
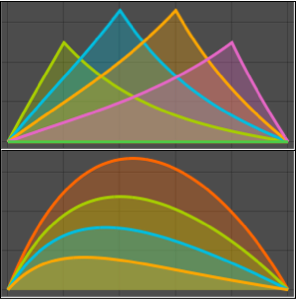
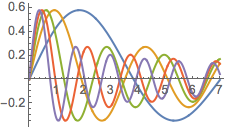
Plotten Sie das Resultat für verschiedene Werte von a.

In[4]:=

InverseMellinTransform[(2^(-1 + s) a^-s Gamma[1/2 + s/2])/ Gamma[3/2 - s/2], s, x]; Plot[Table[% , {a, 1, 5}] // Evaluate, {x, 0, 7}]

Out[4]=

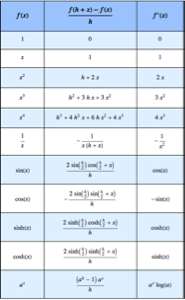
Erzeugen Sie eine Tabelle grundlegender Umkehrungen der Mellin-Transformation.

In[5]:=

flist = {1/s, 1/(s + 1), a^(s - 1), Gamma[s], Gamma[1 - s], \[Pi] Csc[\[Pi] s], Gamma[s] Sin[(\[Pi] s)/2], Cos[(\[Pi] s)/2] Gamma[s], \[Pi] Cot[\[Pi] s], 1/2 Gamma[s/2]}; TraditionalForm[ Simplify[Grid[ Map[Style[#, ScriptLevel -> 0] &, Join[{{HoldForm@f[s], HoldForm@InverseMellinTransform[f[s], s, x]}}, Transpose[{flist, (InverseMellinTransform[#1, s, x] &) /@ flist}]], {2}], Dividers -> All, Spacings -> {4, 2}, Background -> {None, {{None, GrayLevel[.9]}}, {{1, 1} -> Hue[.6, .4, 1], {1, 2} -> Hue[.6, .4, 1]}}, BaseStyle -> {FontFamily -> Times, FontSize -> 13}]]]

Out[5]//TraditionalForm=