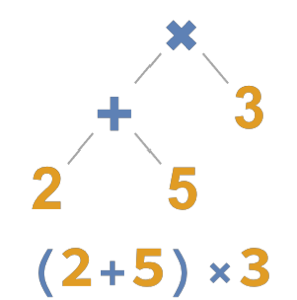
Créez une calculatrice en utilisant une grammaire indépendante du contexte
Déployez une calculatrice simple qui prend en charge la notation infixe, polonaise et polonaise inversée. Utilisez l'élément intégré "SemanticNumber" et définissez des règles pour l'élément personnalisé "Math".
In[1]:=

calc = CloudDeploy[
GrammarRules[{GrammarToken["SemanticNumber"], GrammarToken["Math"]},
{"Math" -> GrammarToken["SemanticNumber"],
"Math" ->
AnyOrder[a : GrammarToken["Math"], "+",
b : GrammarToken["Math"]] :> a + b,
"Math" ->
AnyOrder[a : GrammarToken["Math"], "-",
b : GrammarToken["Math"]] :> a - b,
"Math" ->
AnyOrder[a : GrammarToken["Math"], "*",
b : GrammarToken["Math"]] :> a*b,
"Math" ->
AnyOrder[a : GrammarToken["Math"], "/",
b : GrammarToken["Math"]] :> a/b}
]
];Essayez la calculatrice.
In[2]:=
GrammarApply[calc, "2 3 + * five"]Out[2]=
In[3]:=
GrammarApply[calc, "* * * * 1 2 3 4 5"]Out[3]=
In[4]:=
GrammarApply[calc, "1 2 3 4 5 + + + +"]Out[4]=
En fonction de l'utilisation de la notation polonaise infixe et/ou inversée, il peut y avoir une ambiguïté dans l'analyse de l'entrée. Ceci est géré par l'option AmbiguityFunction. Le résultat 16 correspond à l'analyse syntaxique 2 (3 + 5) *, tandis que le résultat 25 correspond à l'analyse syntaxique (2 3 +) 5 *.
In[5]:=
GrammarApply[calc, "2 3 + 5 *", AmbiguityFunction -> All]Out[5]=