Loi de Zipf

La loi de Zipf indique que dans un corpus d'une langue, la fréquence d'un mot est inversement proportionnelle à son rang dans la liste globale des mots après le tri par ordre décroissant de fréquence. Cet exemple démontre la loi avec l'ensemble des mots dans le roman Don Quichotte de Miguel de Cervantes en utilisant les nouvelles fonctions WordCount et WordCounts.

ExampleData contient le texte en espagnol du premier volume de Don Quichotte.

In[1]:=

textSpanish = ExampleData[{"Text", "DonQuixoteISpanish"}];

L'échantillon considéré ici est constitué de plus de 180 000 mots.

In[2]:=

WordCount[textSpanish]

Out[2]=

Le nombre de chaque mot distinct est donné sous forme d'association par WordCounts. Le résultat est déjà trié par nombre décroissant.

In[3]:=

association = WordCounts[textSpanish];

In[4]:=

Take[association, 10]

Out[4]=

Relevez le nombre des 1000 premiers mots les plus fréquents.

In[5]:=

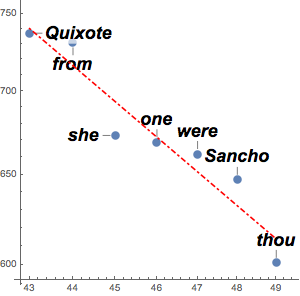
counts = Take[Values@association, 1000];

Pour approximer ces chiffres avec une loi de puissance, prenez les logarithmes pour utiliser l'ajustement linéaire. La loi de Zipf stipule que l'exposant doit être approximativement 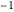et le résultat est une valeur proche.

In[6]:=

f[x_] = Fit[Log[Transpose[{Range[1000], counts}]], {1, x}, x]

Out[6]=

Visualisez l'ajustement avec les données réelles.

In[7]:=

Show[ ListLogLogPlot[counts, PlotStyle -> PointSize[0.02]], LogLogPlot[Exp[f[Log[x]]], {x, 1, 1000}, PlotStyle -> Directive[DotDashed, Red]], AspectRatio -> 1, PlotRange -> All ]

Out[7]=

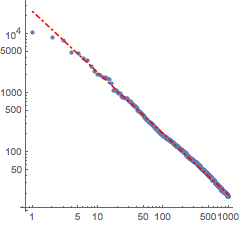
La loi de Zipf s'applique dans n'importe quelle langue, de sorte que le même calcul est effectué avec la version anglaise de Don Quichotte.

In[8]:=

textEnglish = ExampleData[{"Text", "DonQuixoteIEnglish"}];

In[9]:=

associationEnglish = WordCounts[textEnglish]; countsEnglish = Take[Values@associationEnglish, 1000];

In[10]:=

Take[associationEnglish, 10]

Out[10]=

Encore une fois, l'exposant trouvé est proche de .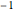

In[11]:=

Fit[Log[Transpose[{Range[1000], countsEnglish}]], {1, x}, x]

Out[11]=