Visualización de datos de huracanes
El modelo simple para un vórtice se da por medio de la combinación de la rotación del cuerpo dentro de un núcleo y la decreciente velocidad angular externa.
muestre la entrada completa de Wolfram Language
In[2]:=
wind[r_, z_] := If[r <= rcore, w r, (w a^2)/r];La fórmula para encontrar presión da la siguiente fórmula en términos de radio y elevación.
In[3]:=
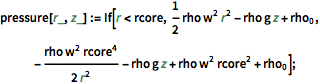
pressure[r_, z_] :=
If[r < rcore,
1/2 rho w^2 r^2 - rho g z + Subscript[rho,
0], -((rho w^2 rcore^4)/(2 r^2)) - rho g z + rho w^2 rcore^2 +
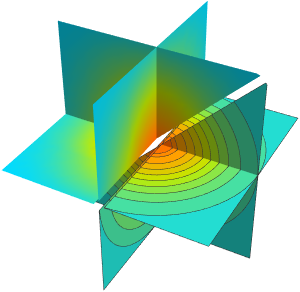
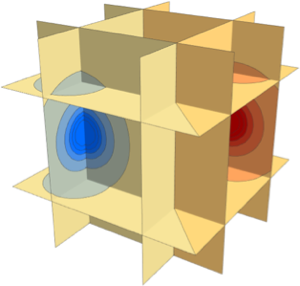
Subscript[rho, 0]];Grafique las velocidades del viento, las cuales aceleran fuera del centro del sistema.
In[4]:=

SliceContourPlot3D[
wind[Sqrt[x^2 + y^2], z], {x^2 + y^2 == 3 z, x^2 + y^2 == 6 z,
x^2 + y^2 == 1 z}, {x, -5, 5}, {y, -5, 5}, {z, 1, 5},
Contours -> 20,
RegionFunction -> Function[{x, y, z}, x < 0 || y > 0],
PlotTheme -> "NoAxes", PlotLegends -> Automatic,
PlotLabel -> "Wind Strength", ImageSize -> 400]Out[4]=

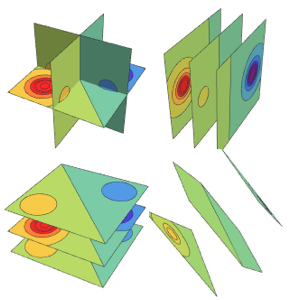
Grafique las direcciones del viento como un campo vectorial.
In[5]:=

SliceVectorPlot3D[{(wind[Sqrt[x^2 + y^2], z] y)/
Norm[{x, y}], (-wind[Sqrt[x^2 + y^2], z] x)/Norm[{x, y}],
0}, {x^2 + y^2 == z, x^2 + y^2 == 3 z, x^2 + y^2 == 6 z}, {x, -5,
5}, {y, -5, 5}, {z, 1, 5}, ImageSize -> 400, PlotLegends -> None,
VectorStyle -> "Arrow3D", VectorScale -> {Medium, 0.5, Automatic},
VectorPoints -> 8,
RegionFunction -> Function[{x, y, z}, x < 0 || y > 0],
PlotTheme -> "NoAxes", PlotLabel -> "Wind Direction"]Out[5]=

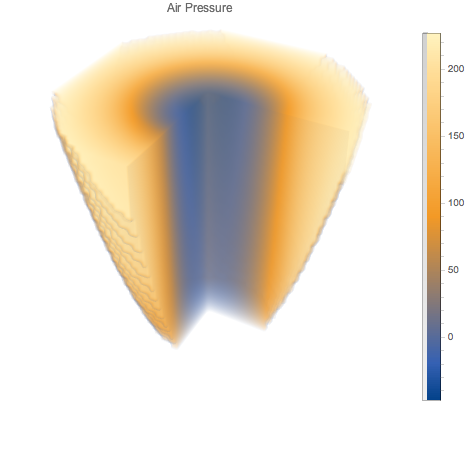
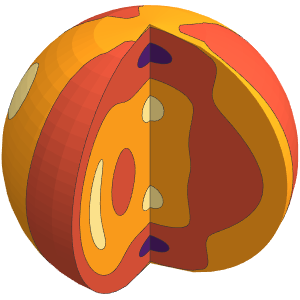
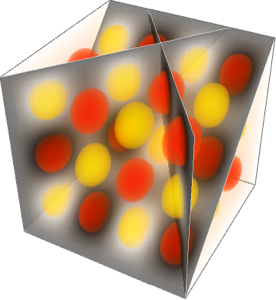
Grafique la presión como una densidad en 3D. Note la presión baja relativa en el centro del sistema.
In[6]:=
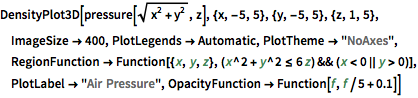
DensityPlot3D[
pressure[Sqrt[x^2 + y^2], z], {x, -5, 5}, {y, -5, 5}, {z, 1, 5},
ImageSize -> 400, PlotLegends -> Automatic, PlotTheme -> "NoAxes",
RegionFunction ->
Function[{x, y, z}, (x^2 + y^2 <= 6 z) && (x < 0 || y > 0)],
PlotLabel -> "Air Pressure",
OpacityFunction -> Function[f, f/5 + 0.1]]Out[6]=