Visualisez des données d'ouragans
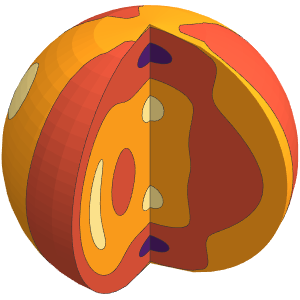
Le modèle le plus simple pour un vortex est donnée par la combinaison de la rotation du corps dans un noyau et la diminution de la vitesse angulaire à l'extérieur.
Afficher l'entrée complète de Wolfram Language
In[2]:=
wind[r_, z_] := If[r <= rcore, w r, (w a^2)/r];La formule pour trouver la pression fournit la formule suivante en termes de rayon et d'élévation.
In[3]:=
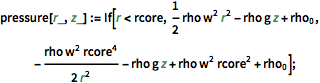
pressure[r_, z_] :=
If[r < rcore,
1/2 rho w^2 r^2 - rho g z + Subscript[rho,
0], -((rho w^2 rcore^4)/(2 r^2)) - rho g z + rho w^2 rcore^2 +
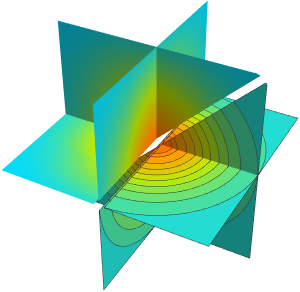
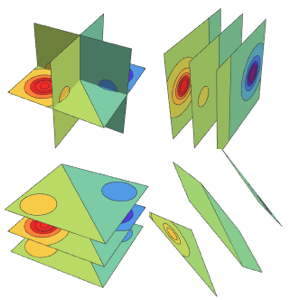
Subscript[rho, 0]];Tracez les vitesses du vent qui se trouvent en dehors du centre le plus rapide du système.
In[4]:=

SliceContourPlot3D[
wind[Sqrt[x^2 + y^2], z], {x^2 + y^2 == 3 z, x^2 + y^2 == 6 z,
x^2 + y^2 == 1 z}, {x, -5, 5}, {y, -5, 5}, {z, 1, 5},
Contours -> 20,
RegionFunction -> Function[{x, y, z}, x < 0 || y > 0],
PlotTheme -> "NoAxes", PlotLegends -> Automatic,
PlotLabel -> "Wind Strength", ImageSize -> 400]Out[4]=

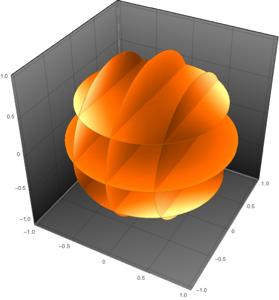
Tracez les directions du vent en tant que champ vectoriel.
In[5]:=

SliceVectorPlot3D[{(wind[Sqrt[x^2 + y^2], z] y)/
Norm[{x, y}], (-wind[Sqrt[x^2 + y^2], z] x)/Norm[{x, y}],
0}, {x^2 + y^2 == z, x^2 + y^2 == 3 z, x^2 + y^2 == 6 z}, {x, -5,
5}, {y, -5, 5}, {z, 1, 5}, ImageSize -> 400, PlotLegends -> None,
VectorStyle -> "Arrow3D", VectorScale -> {Medium, 0.5, Automatic},
VectorPoints -> 8,
RegionFunction -> Function[{x, y, z}, x < 0 || y > 0],
PlotTheme -> "NoAxes", PlotLabel -> "Wind Direction"]Out[5]=

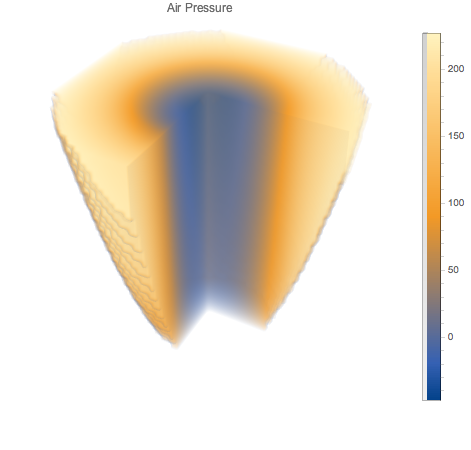
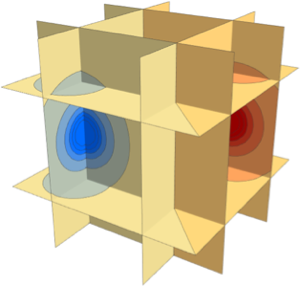
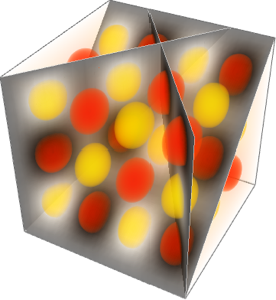
Tracez la pression en tant que densité en 3D. Remarquez la faible pression relative au centre du système.
In[6]:=
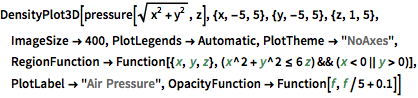
DensityPlot3D[
pressure[Sqrt[x^2 + y^2], z], {x, -5, 5}, {y, -5, 5}, {z, 1, 5},
ImageSize -> 400, PlotLegends -> Automatic, PlotTheme -> "NoAxes",
RegionFunction ->
Function[{x, y, z}, (x^2 + y^2 <= 6 z) && (x < 0 || y > 0)],
PlotLabel -> "Air Pressure",
OpacityFunction -> Function[f, f/5 + 0.1]]Out[6]=