Visualisez les fonctions propres

Définissez un opérateur de Laplace en 3D.

In[1]:=

\[ScriptCapitalL] = -Laplacian[u[x, y, z], {x, y, z}];

Précisez des conditions aux limites de Dirichlet homogènes.

In[2]:=

\[ScriptCapitalB] = DirichletCondition[u[x, y, z] == 0, True];

Trouvez les plus petites valeurs propres et fonctions propres dans une balle.

In[3]:=

\[CapitalOmega] = Ball[{0, 0, 0}, 2]; {vals, funs} = DEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]}, u[x, y, z], {x, y, z} \[Element] \[CapitalOmega], 2];

In[4]:=

funs

Out[4]=

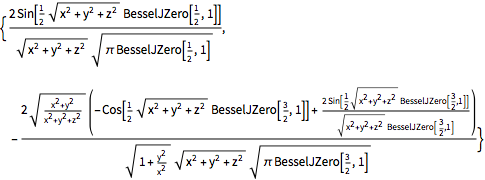
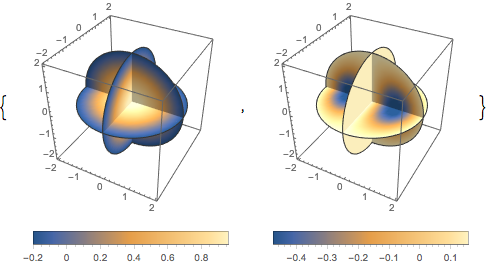
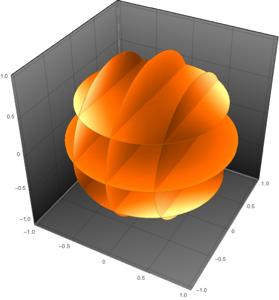
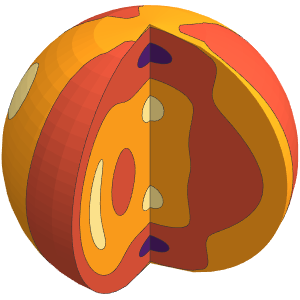
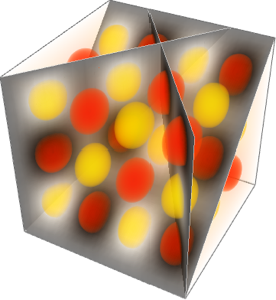
Tracez chaque fonction propre en utilisant un tracé de densité 3D.

In[5]:=

Table[DensityPlot3D[ Evaluate[N[f]], {x, y, z} \[Element] \[CapitalOmega], PlotTheme -> "NoAxes", PlotLegends -> Placed[Automatic, Below]], {f, funs}]

Out[5]=

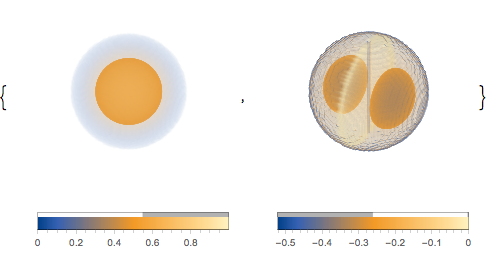
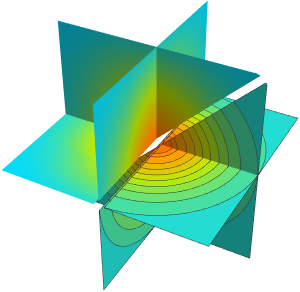
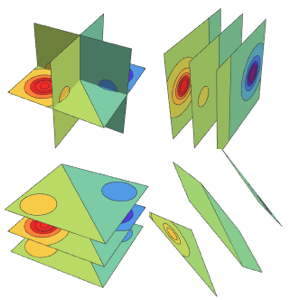
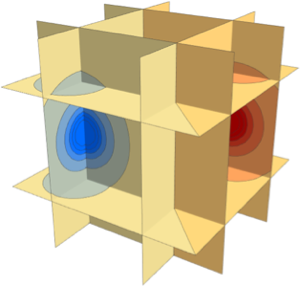
Utilisez des plans de coordonnées pour tracer la densité.

In[6]:=

Table[SliceDensityPlot3D[ Evaluate[N[f]], {x, y, z} \[Element] \[CapitalOmega], PlotLegends -> Placed[Automatic, Below]], {f, funs}]

Out[6]=