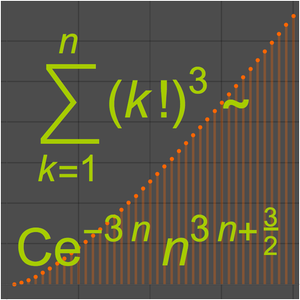
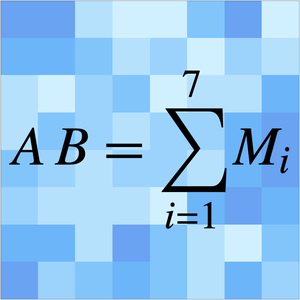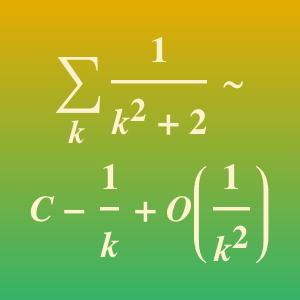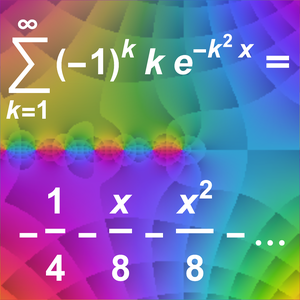Find a Taylor Expansion for an Exponential Sum (AsymptoticSum)
Asymptotic methods can give useful approximations for infinite sums that depend on a parameter. This example shows how an infinite exponential sum can be approximated with a Taylor expansion in terms of the parameter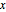 
in the summand. The coefficients of the Taylor series are obtained by computing the residues at the poles of the Mellin transform for this sum.
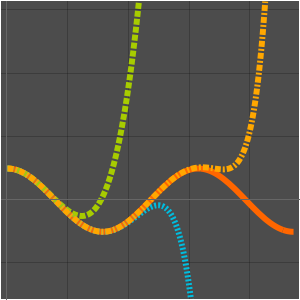
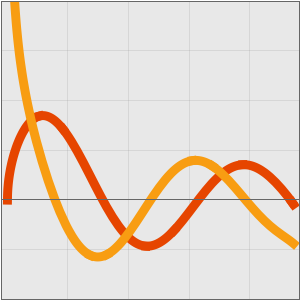
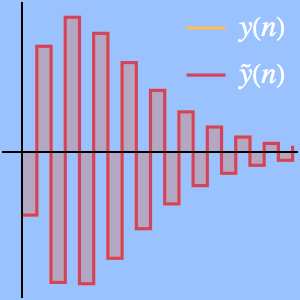
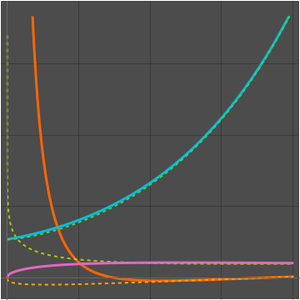
Find a Taylor approximation for an alternating Gaussian exponential sum.
Compare with a numerical approximation.
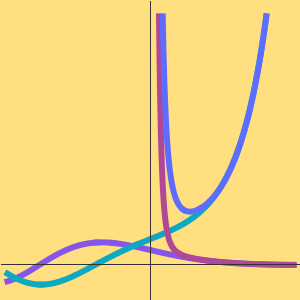
The asymptotic approximation relies on a Mellin transform computation.
The coefficients of the Taylor series are computed using the poles of the sum.
