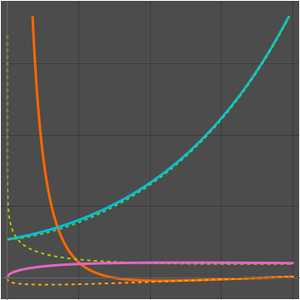
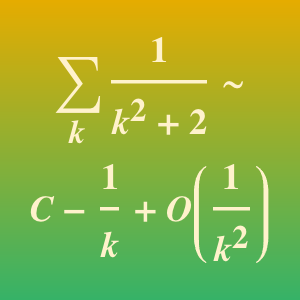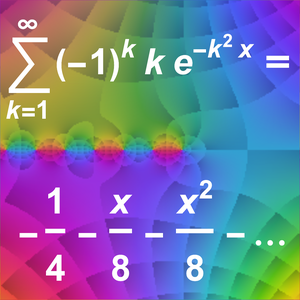지수합의 테일러 전개 구하기(AsymptoticSum)
점근법은 매개변수에 의존하는 무한합에 유용한 근사를 제공할 수 있습니다. 이 예는 무한의 지수합이 피가수의 매개변수 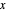 에 대해 테일러 전개에서 어떻게 근사할 수 있는지를 보여줍니다. 테일러 급수의 계수는 이 합의 멜린(Mellin) 변환의 극에 있어서의 나머지를 계산함으로써 얻을 수 있습니다.
에 대해 테일러 전개에서 어떻게 근사할 수 있는지를 보여줍니다. 테일러 급수의 계수는 이 합의 멜린(Mellin) 변환의 극에 있어서의 나머지를 계산함으로써 얻을 수 있습니다.
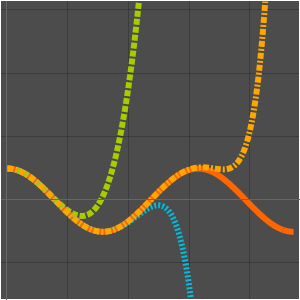
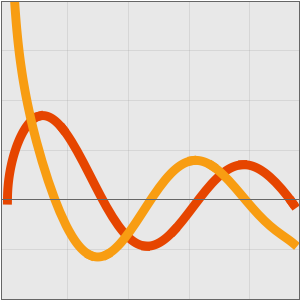
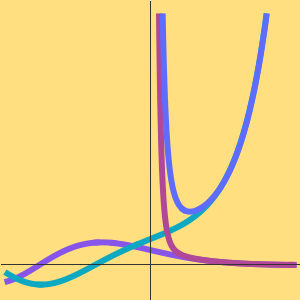
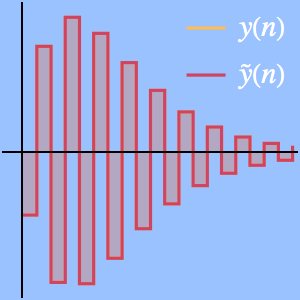
가우스의 지수형 교화합의 테일러 근사를 구합니다.
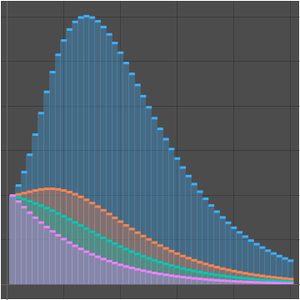
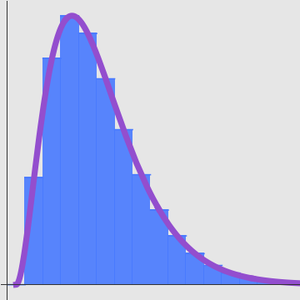
수치 근사와 비교합니다.
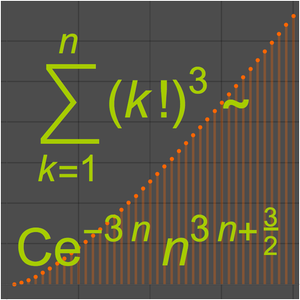
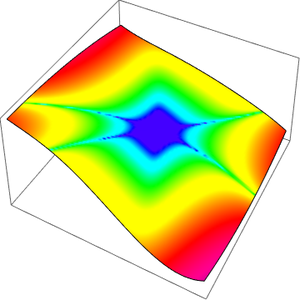
점근 근사는 멜린 변환의 계산에 의존합니다.
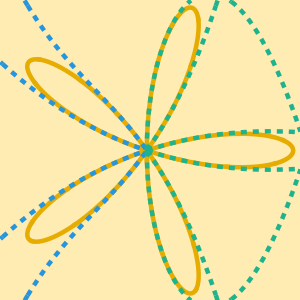
테일러 급수의 계수는 총합의 극을 사용하여 계산됩니다.