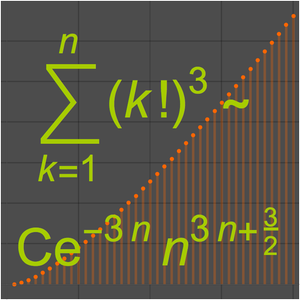
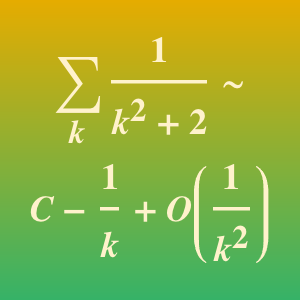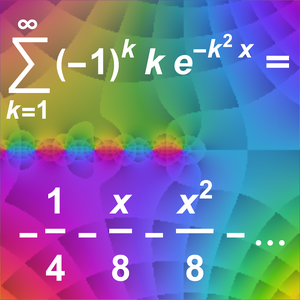Recherchez un développement de Taylor pour une somme exponentielle (AsymptoticSum)
Les méthodes asymptotiques peuvent donner des approximations utiles pour des sommes infinies qui dépendent d'un paramètre. Cet exemple démontre comment une somme exponentielle infinie peut être approximée avec un développement de Taylor en fonction du paramètre 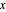 dans l'opérande. Les coefficients de la série de Taylor sont obtenus en calculant les résidus aux pôles de la transformation de Mellin pour cette somme.
dans l'opérande. Les coefficients de la série de Taylor sont obtenus en calculant les résidus aux pôles de la transformation de Mellin pour cette somme.
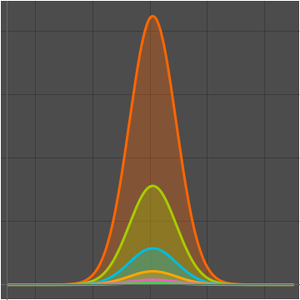
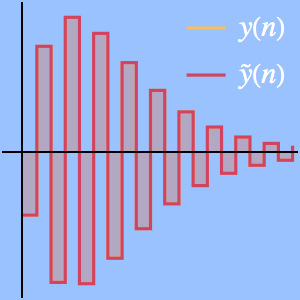
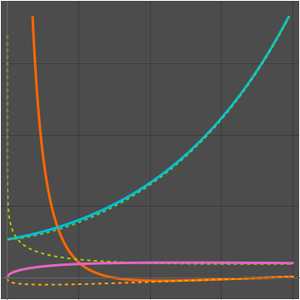
Recherchez une approximation de Taylor pour une somme exponentielle gaussienne alternée.
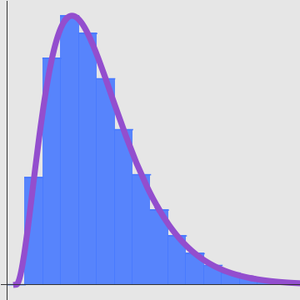
Comparez avec une approximation numérique.
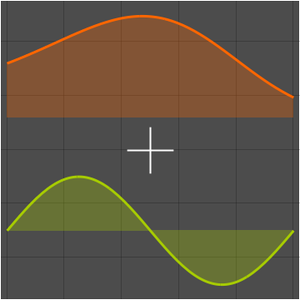
L'approximation asymptotique repose sur un calcul de la transformation de Mellin.
Les coefficients de la série de Taylor sont calculés à l'aide des pôles de la somme.