Gerschgorin-Kreisscheiben

Das Gerschgorin-Theorem (http://mathworld.wolfram.com/GershgorinCircleTheorem.html) besagt, dass jeder Eigenwert der quadratischen Matrix 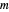in mindestens einer der Scheiben ist, deren Mittelpunkt die Diagonaleingänge von 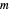sind und deren Radien eine Summe der Einträge in jeder Zeile sind.

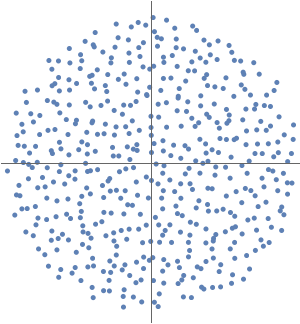
Generieren Sie eine komplexe Zufallsmatrix .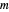

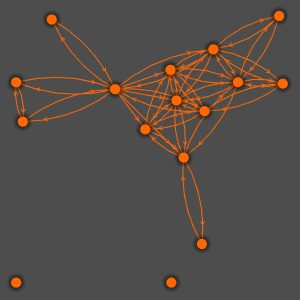
Die Diagonaleinträge von 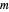sind die Mittelpunkte der Gerschgorin-Kreisscheiben.

Der Radius der 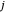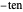Gerschgorin-Scheibe, 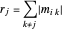, ist gegeben durch die betragsmäßige Summe der Einträge der Zeile 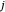, außer dem Diagonaleintrag.

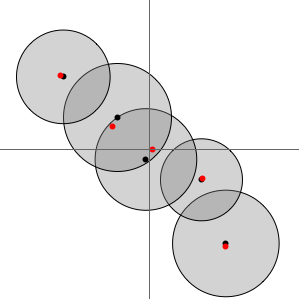
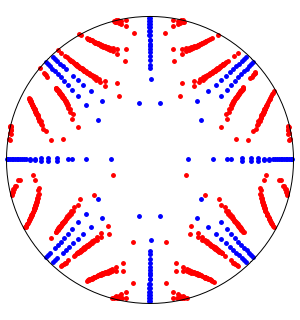
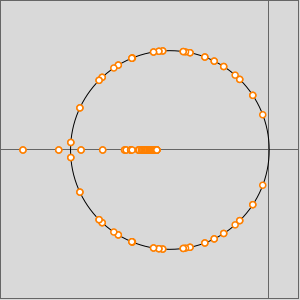
Erstellen Sie die Gerschgorin-Scheiben der Matrix.

Veranschaulichen Sie die Eigenwerte (rechts) in den Gerschgorin-Scheiben.