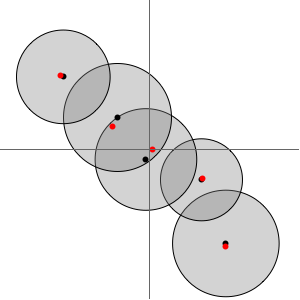
ゲルシュゴリン(Gerschgorin)円板

ゲルシュゴリンの定理(http://mathworld.wolfram.com/GershgorinCircleTheorem.html)によると，正方行列 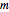の固有値はどれも，中心が 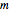の対角成分であり半径が各行の成分の和である円板のうちの少なくとも一つの円板上にある．

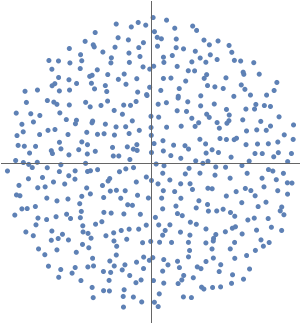
ランダムな複素行列 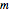を生成する．

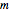の対角成分は，ゲルシュゴリン円板の中心である．

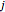番目のゲルシュゴリン円板の半径 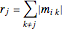は，対角成分を除く行 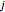の成分の絶対値の総和である．

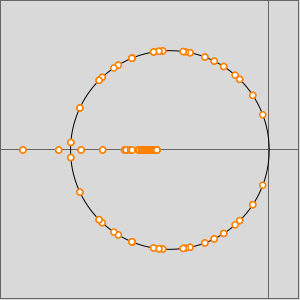
行列のゲルシュゴリン円板を作成する．

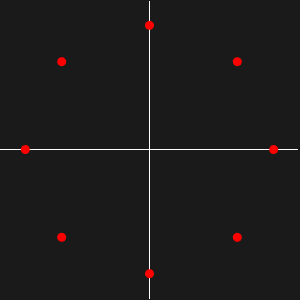
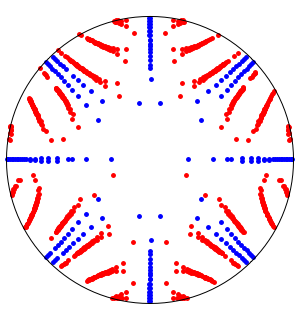
ゲルシュゴリン円板の固有値（赤）を表示する．