特徴を視覚的に識別する
複素関数のいくつもの特徴をプロットから識別することができる．
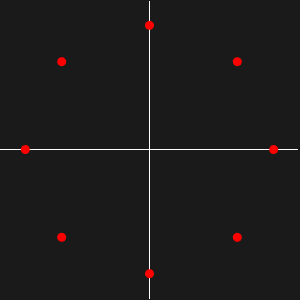
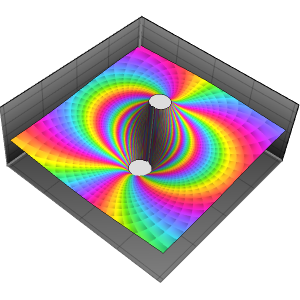
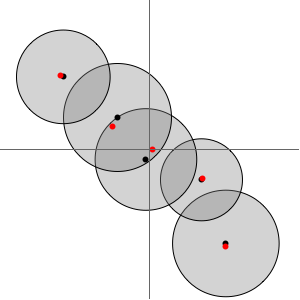
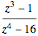のプロットを見ると，1の三乗根に零点があり，
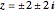に4つの極があることが分かる．
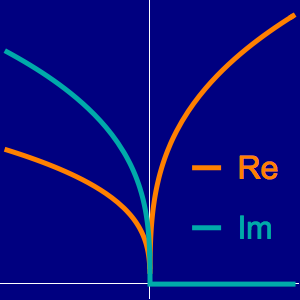
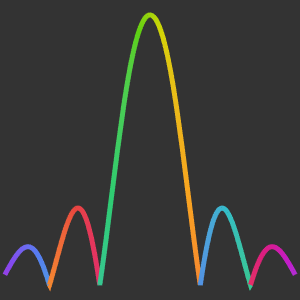
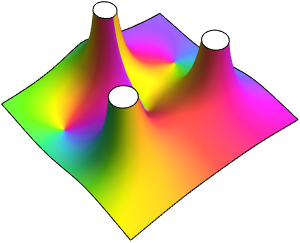
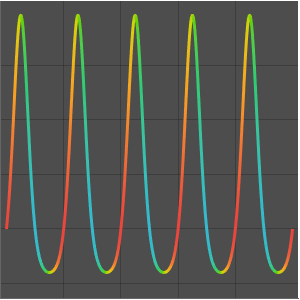
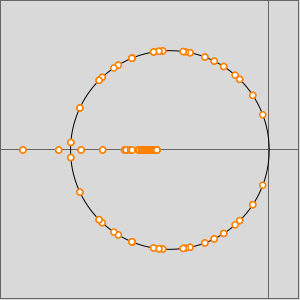
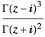のプロットから，
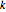が非負の整数の場合 
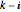に二次の零点があり，
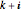に三次の極があることが分かる．
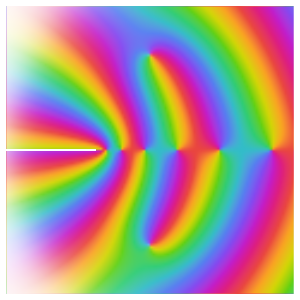
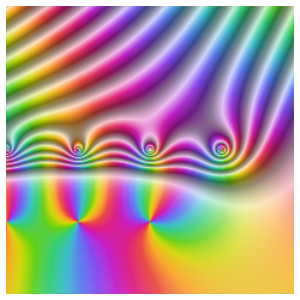
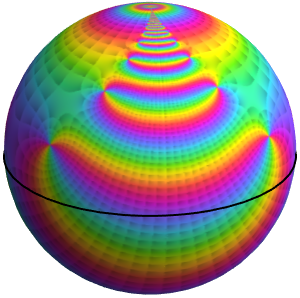
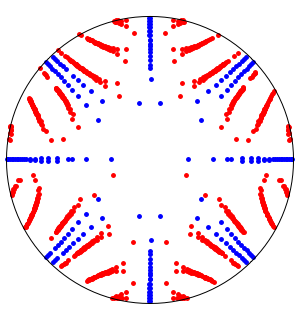
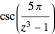のプロットはさらに複雑な挙動を示す．これを見ると，零点はないが， 
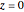において三次の極があることが分かる．また
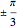と 
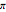のそれぞれの角に沿って，次数1の極が4つある．また，角0と
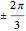に沿って，
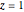と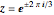 
における真性特異点で集積する次数1の極がある．
