Soluciones de ecuaciones diferenciales ordinarias complejas
Resuelva la ecuación diferencial ordinaria compleja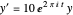 
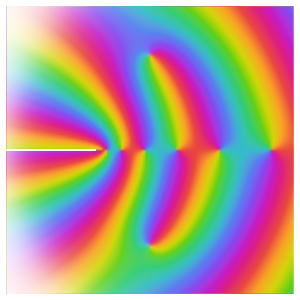
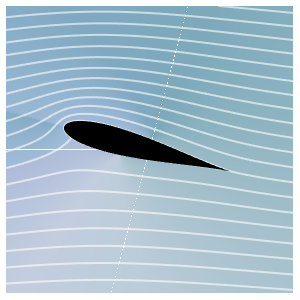
con la condición inicial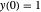 
y visualice el comportamiento.
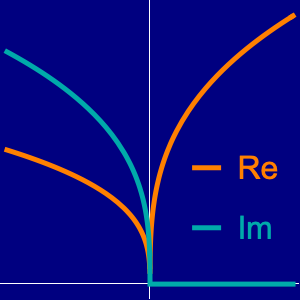
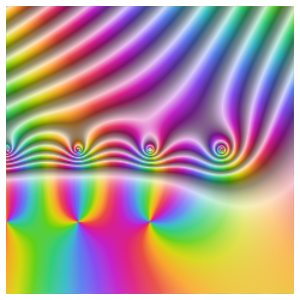
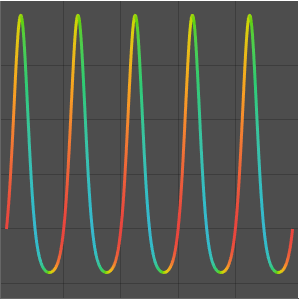
Represente gráficamente las partes reales e imaginarias de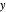 
como una función de la variable real 
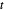. Ambas partes son oscilatorias, pero el componente imaginario permanece positivo en su mayoría, mientras que la parte real es simétrica con respecto a cero.
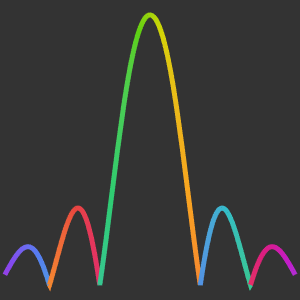
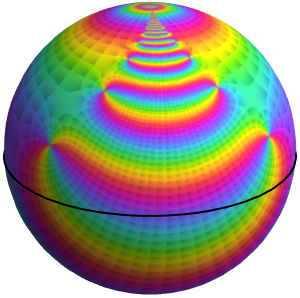
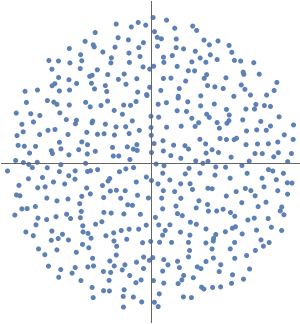
Grafique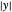 
como una función de la variable real 
.
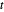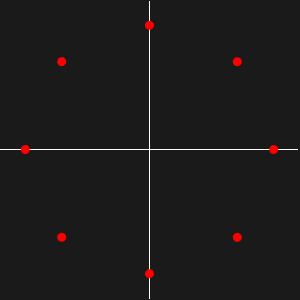
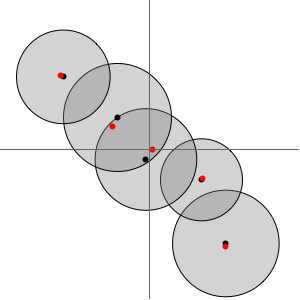
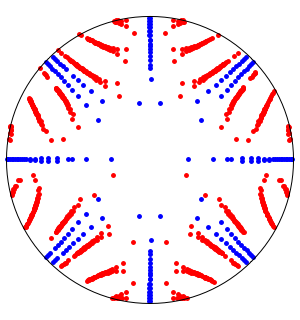
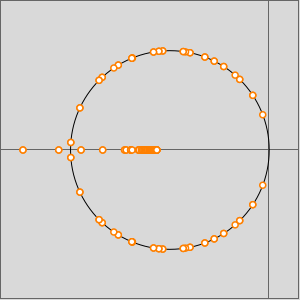
Grafique la solución paramétricamente en el plano complejo con un muestreo en valores distintos de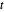 
.
muestre la entrada completa de Wolfram Language
