Visualización de valores propios de grafos
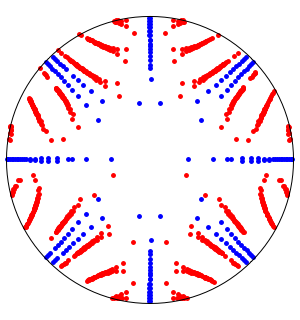
Los valores propios de grafos pueden darnos información acerca de sus propiedades estructurales.
Genere un grafo dirigido acíclico a partir de un grafo base.
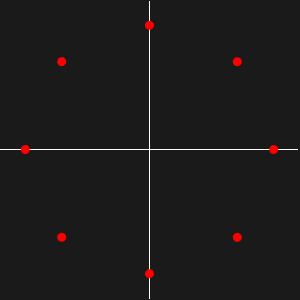
Si un grafo es acíclico, entonces su matriz de adyacencia es nilpotente y todos sus valores propios son cero.
Si un grafo es simétrico, entonces su matriz de adyacencia es simétrica y sus valores propios son reales.
Si un grafo es bipartito, entonces el espectro de su matriz de adyacencia es rotacionalmente simétrico con respecto a 0. Es decir, si 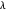 es un valor propio de la matriz de adyacencia, entonces también lo es
es un valor propio de la matriz de adyacencia, entonces también lo es 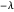 .
.
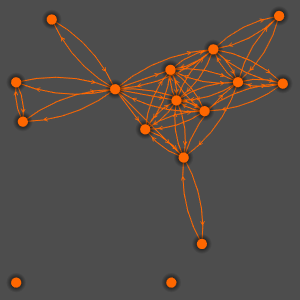
Genere un grafo que muestre un conjunto de símbolos que se conecten uno con otro en la documentación Wolfram.
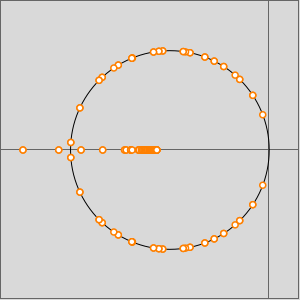
El gráfico de los valores propios del grafo muestra que hay ciclos presentes, pero que el grafo no es ni simétrico ni bipartito.
El grafo no es simétrico porque ComplexExpand se conecta con Complex, Conjugate, Im, y Re, pero no a la inversa.