Eigenvalue Optimization
Find linear combinations of symmetric matrices that optimize various properties relating to the eigenvalues of the combinations.
This example demonstrates how semidefinite constraints (that are effectively constraints on eigenvalues) may be used in different ways with SemidefiniteOptimization to solve eigenvalue optimization problems.
Find 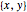 that minimizes the largest eigenvalue of a symmetric matrix
that minimizes the largest eigenvalue of a symmetric matrix 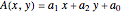 .
.
The problem can be formulated as a linear matrix inequality since 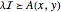 is equivalent to
is equivalent to 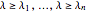 , where
, where 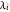 is the
is the  th eigenvalue of
th eigenvalue of 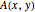 .
.
Construct the matrix with the maximal eigenvalue.
Compute its eigenvalues
Show the solution on a plot of the maximum eigenvalue as a function of 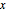 and
and 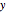 .
.
Run a Monte Carlo simulation to check the plausibility of the result.
Solve some similar problems. Maximize the smallest eigenvalue.
Minimize the difference between the largest and the smallest eigenvalue.
Minimize the largest eigenvalue by the absolute value eigenvalue (or the spectral norm).
In principle, this works for a combination of any number of matrices of any size.