Eigenwert-Optimierung
Finden Sie lineare Kombinationen von symmetrischen Matrizen, die verschiedene Eigenschaften in Bezug auf die Eigenwerte der Kombinationen optimieren.
Dieses Beispiel zeigt, wie ein semidefinites Programm (Einschränkungen von Eigenwerten) mit SemidefiniteOptimization auf verschiedene Weise verwendet werden kann, um Eigenwertoptimierungsprobleme zu lösen.
Ermitteln Sie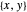 
das den größten Eigenwert einer symmetrischen Matrix 
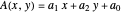minimiert.
Das Problem kann als lineare Matrixungleichheit formuliert werden, da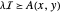 
gleichbedeutend ist mit 
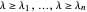, wobei 
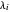der 
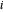
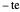Eigenwert von 
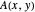ist.
Bilden Sie die Matrix mit dem maximalen Eigenwert.
Berechnen Sie ihre Eigenwerte.
Veranschaulichen Sie die Lösung auf einem Plot des maximalen Eigenwertes als Funktion von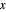 
und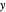 
.
Führen Sie eine Monte-Carlo-Simulation durch, um die Plausibilität des Ergebnisses zu überprüfen.
Lösen Sie weitere ähnliche Probleme. Maximieren Sie den kleinsten Eigenwert.
Minimieren Sie die Differenz zwischen dem größten und dem kleinsten Eigenwert.
Minimieren Sie den größten Eigenwert durch den Eigenwert mit dem größten Absolutwert (oder der Spektralnorm).
Im Prinzip funktioniert dies bei einer Kombination aus einer beliebigen Anzahl von Matrizen beliebiger Größe.
