固有値最適化
対称行列の線形結合の固有値に関するさまざまな性質を最適化するような線形結合の重み付けを得る.
この例では,さまざまな形で半正定値制約条件(実質的に固有値に対する制約条件)をSemidefiniteOptimizationと一緒に使って,固有値最適化問題を解く方法を説明する.
対称行列 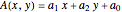 の最大の固有値を最小化する
の最大の固有値を最小化する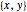 を求める.
を求める.
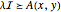 が
が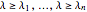 (
(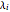 は
は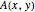 の
の 
 番目の固有値)と等しいので,この問題は線形行列不等式として定式化することができる.
番目の固有値)と等しいので,この問題は線形行列不等式として定式化することができる.
最大の固有値で行列を構築する.
その固有値を計算する.
最大固有値のプロット上に,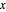 と
と 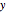 の関数として解を表示する.
の関数として解を表示する.
モンテカルロシミュレーションを実行し,結果の妥当性を検証する
同様の問題を解いてみよう.最小の固有値を最大化する.
最大の固有値と最小の固有値の差分を最小化する.
絶対値固有値(スペクトルノルム)によって最大の固有値を最小化する.
原則として,これはあらゆるサイズのあらゆる数の行列の組合せで使える.