Optimisation de la valeur propre
Trouvez des combinaisons linéaires de matrices symétriques qui optimisent diverses propriétés se rapportant aux valeurs propres des combinaisons.
Cet exemple démontre comment les contraintes semi-définies (qui sont effectivement des contraintes sur les valeurs propres) peuvent être utilisées de différentes manières avec SemidefiniteOptimization pour résoudre les problèmes d'optimisation des valeurs propres.
Déterminez 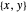 qui minimise la plus grande valeur propre d'une matrice symétrique
qui minimise la plus grande valeur propre d'une matrice symétrique 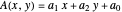 .
.
Le problème peut être formulé comme une inégalité matricielle linéaire puisque 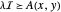 est équivalent à
est équivalent à 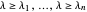 , où
, où 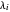 correspond à la valeur propre
correspond à la valeur propre 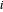 th de
th de 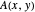 .
.
Construisez la matrice avec la valeur propre maximale.
Calculez ses valeurs propres.
Représentez graphiquement la solution de la valeur propre maximale en fonction de 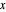 et
et 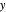 .
.
Exécutez une simulation Monte Carlo pour vérifier la plausibilité du résultat.
Résolvez des problèmes similaires. Maximisez la plus petite valeur propre.
Minimisez la différence entre la plus grande et la plus petite valeur propre.
Minimisez la plus grande valeur propre par la valeur propre absolue (ou la norme spectrale).
En principe, cela fonctionne pour une combinaison de n'importe quel nombre de matrices de n'importe quelle taille.