Cuboïde de volume maximal
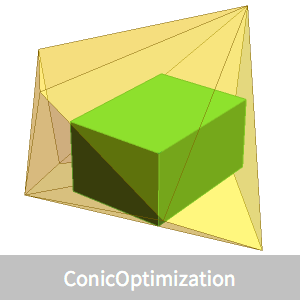
Déterminez le cuboïde de volume maximal parallèle à l'axe, inscrit dans un polyèdre convexe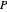 
.
Cet exemple démontre comment l'optimisation d'un produit de termes positifs peut être exprimée en termes de contraintes du cône de puissance pouvant être utilisées avec ConicOptimization pour trouver l'optimum.
Prenons un polyèdre convexe aléatoire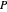 
construit comme l'enveloppe convexe de points aléatoires.
Pour le cuboïde, trouvez un point de coin inférieur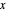 
et un vecteur de longueur latérale 
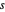de sorte que le cuboïde soit représenté dans Wolfram Language par 
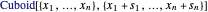. Le volume du cuboïde correspond uniquement au produit des longueurs des côtés, l'objectif est donc de maximiser 
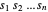. Si tous les coins du cuboïde se trouvent dans 
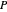, alors tous les points du cuboïde s'y trouvent également. Les coins peuvent être décrits par 
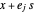, où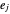 
se trouve dans l'ensemble 
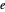de tous les n‐tuples possibles des éléments de 
.
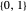Le problème devient :
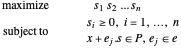
Puisque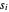 
n'est pas négatif, maximiser le produit 
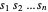est la même chose que de maximiser la moyenne géométrique 
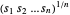, qui est reconnue comme concave. Maximiser 
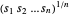équivaut à minimiser 
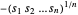, qui est convexe. À l'aide d'une variable auxiliaire 
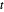, reformulez le problème avec une fonction-objectif linéaire -
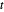avec les contraintes supplémentaires 
.
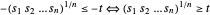Le problème devient :
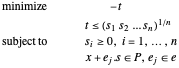
Le cône de puissance représente l'ensemble de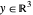 
de sorte que 
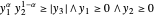, et peut être exprimé dans Wolfram Language par 
.
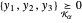Puisque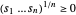 
, la nouvelle contrainte 
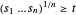peut être satisfaite pour 
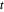non négatif et est équivalente à 
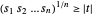. On peut l'écrire comme une série de contraintes de cône de puissance :
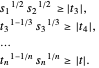
Pour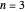 
le problème devient :
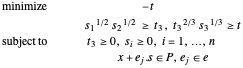
Un polyèdre convexe peut être représenté sous la forme d'intersections de demi-espaces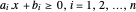 
. Extrayez les coefficients 
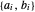de chaque côté.
Résolvez le problème.
Affichez le cuboïde de volume maximal inscrit.
Au lieu d'un polyèdre, prenez n'importe quel ensemble conique convexe K⊆n représentable, par exemple, un ellipsoïde. Un sommet du cuboïde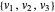 
se trouve à l'intérieur de l'ellipsoïde si 
.
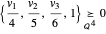Résolvez le problème.
Représentez graphiquement le résultat.
