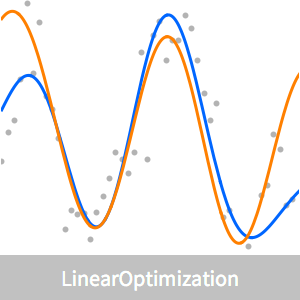
Poursuite de base
Pour un ensemble de fonctions de base 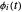 , un signal
, un signal 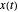 peut être approximé par la combinaison linéaire
peut être approximé par la combinaison linéaire 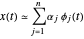 . Généralement, plus la base est grande, plus le signal peut être approximé. Cependant, tous les signaux n'ont pas besoin de toutes les fonctions de base pour une approximation raisonnable. L'idée de la poursuite de base est de choisir un petit sous-ensemble dans un ensemble (ou dictionnaire) plus large de fonctions de base qui peuvent être surdéterminées.
. Généralement, plus la base est grande, plus le signal peut être approximé. Cependant, tous les signaux n'ont pas besoin de toutes les fonctions de base pour une approximation raisonnable. L'idée de la poursuite de base est de choisir un petit sous-ensemble dans un ensemble (ou dictionnaire) plus large de fonctions de base qui peuvent être surdéterminées.
Cet exemple démontre comment la poursuite de base peut être effectuée facilement et efficacement en utilisant Fit avec l'option FitRegularization.
Pour les signaux à échantillonnage temporel discret, la reconstruction peut simplement être donnée sous la forme d'une équation matricielle 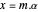 , où
, où 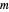 correspond à la matrice avec les éléments
correspond à la matrice avec les éléments 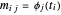 . Pour les bases surdéterminées, les coefficients α, qui donnent la meilleure approximation, peuvent simplement être trouvés par les moindres carrés. Si, au lieu de minimiser
. Pour les bases surdéterminées, les coefficients α, qui donnent la meilleure approximation, peuvent simplement être trouvés par les moindres carrés. Si, au lieu de minimiser 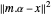 , un terme de régularisation L1 est ajouté pour donner
, un terme de régularisation L1 est ajouté pour donner 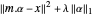 , des valeurs suffisamment grandes du paramètre
, des valeurs suffisamment grandes du paramètre 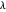 incite les composantes α a être égale à zéro. Le problème peut être résolu efficacement en utilisant Fit avec la nouvelle option FitRegularization.
incite les composantes α a être égale à zéro. Le problème peut être résolu efficacement en utilisant Fit avec la nouvelle option FitRegularization.
Utilisez une base de fonctions de Gabor 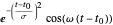 et
et 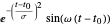 comme exemple d'un grand dictionnaire de fonctions de base.
comme exemple d'un grand dictionnaire de fonctions de base.
Voici un tracé montrant un échantillon des fonctions de Gabor.
Dans l'intervalle de 0 à 1 avec un intervalle d'échantillonnage temporel 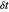 , un ensemble de fonctions de base avec
, un ensemble de fonctions de base avec 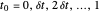 ,
, 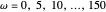 et un
et un 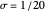 fixe sont suffisants pour représenter exactement une grande variété de signaux.
fixe sont suffisants pour représenter exactement une grande variété de signaux.
La matrice de base peut être construite avec DesignMatrix.
Cette matrice est très grande, mais avec une faible perte de précision de représentation, il est possible d'utiliser le fait que les fonctions de Gabor se désintègrent rapidement à partir de 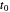 pour la rendre creuse en utilisant un seuil.
pour la rendre creuse en utilisant un seuil.
Considérons maintenant un signal.
Le signal peut être discrétisé en évaluant simplement les échantillons à tout moment.
L'ajustement des moindres carrés indiquera dans quelle mesure la fonction peut être représentée par les fonctions de base. Cela prend beaucoup de temps parce que la matrice est très grande.
L'erreur de représentation complète est effectivement l'arrondi de précision de la machine.
Utilisez maintenant la régularisation L1 pour trouver un ajustement creux. C'est en fait plus rapide à calculer que l'ajustement des moindres carrés, puisqu'il utilise un algorithme creux.
La représentation creuse n'utilise que 50 des 30 561 éléments de base. C'est assez petit pour obtenir une forme fonctionnelle.
Affichez l'erreur.
L'ajustement peut être légèrement amélioré en utilisant la méthode des moindres carrés avec seulement ces éléments de base.
L'erreur peut être réglée en modifiant le paramètre 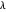 . En général, plus la valeur
. En général, plus la valeur 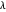 est élevée, moins il y a de fonctions de base et plus il y a d'erreurs, alors que plus la valeur
est élevée, moins il y a de fonctions de base et plus il y a d'erreurs, alors que plus la valeur 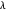 est petite, plus il y aura de fonctions de base et moins il y aura d'erreurs. Voici les diagrammes d'erreurs pour les autres choix de
est petite, plus il y aura de fonctions de base et moins il y aura d'erreurs. Voici les diagrammes d'erreurs pour les autres choix de 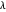 :
: