Problème d'optimisation structurelle
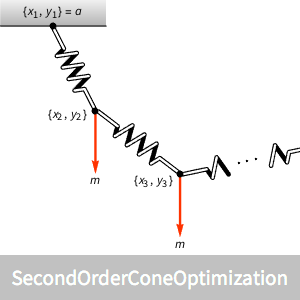
Déterminez la forme d'une chaîne suspendue formée de plusieurs maillons à ressort, avec une masse à chaque jonction de maillons.
Cet exemple démontre comment une condition d'énergie minimale pour l'équilibre peut être exprimée en termes de problème d'optimisation avec des contraintes de cône de second ordre (norme) qui peuvent facilement être résolues avec SecondOrderConeOptimization.
Déterminez la forme d'une chaîne suspendue formée par  maillons à ressort sous une charge verticale à l'extrémité de chaque maillon. L'objectif est de trouver les positions des maillons
maillons à ressort sous une charge verticale à l'extrémité de chaque maillon. L'objectif est de trouver les positions des maillons 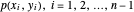 en fonction des positions aux extrémités,
en fonction des positions aux extrémités, 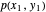 et
et 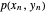 .
.
L'énergie potentielle due à la gravité, sans tenir compte du poids des ressorts, est 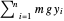 , où
, où 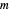 correspond à la charge verticale à chaque extrémité, et
correspond à la charge verticale à chaque extrémité, et 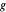 correspond à la gravité standard.
correspond à la gravité standard.
L'énergie potentielle due à la tension du maillon à ressort causée par l'étirement est 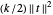 , où
, où 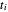 correspond à l'étirement du maillon à ressort
correspond à l'étirement du maillon à ressort 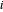 , et
, et 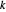 correspond à la rigidité de ce dernier. En utilisant
correspond à la rigidité de ce dernier. En utilisant 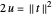 , l'énergie est transformée en
, l'énergie est transformée en 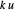 .
.
Une contrainte supplémentaire  doit être ajoutée en raison de la transformation.
doit être ajoutée en raison de la transformation.
Les extrémités de la chaîne à maillons sont maintenues aux positions 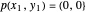 et
et 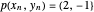 .
.
Puisque 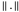 est convexe, il suffit que chaque ressort remplisse la condition
est convexe, il suffit que chaque ressort remplisse la condition 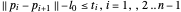 , où
, où 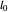 correspond à la longueur au repos de chaque ressort.
correspond à la longueur au repos de chaque ressort.
Les paramètres du design sont illustrés comme suit.
La fonction-objectif finale correspond à la somme de la gravité et de l'énergie potentielle du ressort qui doit être réduite au minimum.
Déterminez les points d'extrémité de chaque maillon à ressort.
Visualisez la forme de la chaîne à ressort obtenue.
Les maillons situés à proximité des extrémités de la chaîne sont les plus tendus. Les maillons 11 et 12 ont l'allongement le plus faible.
La solution est assez rapide pour manipuler le nombre de maillons et les extrémités.