Optimisation du plan de sol
Considérons le problème de placer 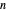 rectangles plus petits à l'intérieur d'un rectangle plus grand de périmètre minimal avec comme contraintes : l'emplacement relatif, le rapport d'aspect, l'espacement entre les petits rectangles et leur superficie.
rectangles plus petits à l'intérieur d'un rectangle plus grand de périmètre minimal avec comme contraintes : l'emplacement relatif, le rapport d'aspect, l'espacement entre les petits rectangles et leur superficie.
Cet exemple démontre l'utilisation de Wolfram Language pour définir une fonction qui utilise NMinimize pour résoudre des problèmes du plan de sol. La fonction utilise des inégalités vectorielles, y compris une inégalité semi-définie.
Soit le plus grand rectangle Rectangle[{0, 0}, {H, W}] et chacun des plus petits ri=Rectangle[{xi, yi}, {xi+wi, yi+hi}], i=1 … n .
Le placement relatif peut être décrit par deux graphes dirigés, un pour le placement horizontal et un pour le placement vertical. S'il y a un bord ij, alors ri doit se trouver à gauche (ou en dessous) de rj.
Pour simplifier, supposons que tous les rectangles doivent avoir un rapport d'aspect entre 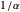 et
et 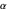 pour
pour 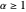 , et que l'espacement entre les rectangles est de
, et que l'espacement entre les rectangles est de 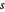 .
.
Compte tenu de ces entrées et d'une liste des zones des petits rectangles, on peut définir une fonction planFloor qui détermine le périmètre minimal du grand rectangle.
Créez des graphes pour l'emplacement relatif de 10 petits rectangles.
Exigez que les superficies de tous les petits rectangles soient de 100, à l'exception d'un rectangle qui a une superficie de 400.
Ceci permet d'optimiser le plan de sol.
Affichez le plan optimal.
Cela montre que la contrainte de superficie est satisfaite avec l'égalité.
Comparez les agencements lorsque les zones sont aléatoires.