Wolfram Language™

Design optimal de poutrelle

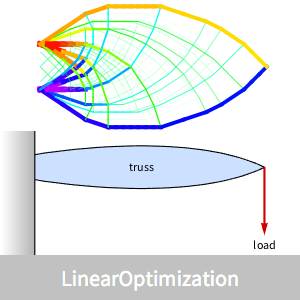
Concevez une poutrelle d'un poids minimal qui est ancrée d'un côté du mur et qui doit résister à une charge de l'autre côté.

Cet exemple démontre combien de caractéristiques de Wolfram Language peuvent être utilisées ensemble pour constituer une forme symbolique d'un problème d'optimisation linéaire qui peut être résolu efficacement par LinearOptimization.

Choisissez quelques positions spécifiques d'où la poutrelle est ancrée au mur.

La position où la charge est appliquée se trouve à l'extrémité de la poutrelle.

La poutrelle peut être modélisée à l'aide de liens et de nœuds. Chaque nœud est relié à un nœud voisin par un lien. Un schéma de liens possibles est donné ici.

Les nœuds potentiels sont placés dans une grille rectangulaire.

Visualisez les positions des nœuds, les positions des points d'ancrage, la position où la force est appliquée et la connectivité d'un nœud unique au milieu de la poutrelle.

Chaque nœud est associé à un index unique. Association fournit efficacement un tableau de recherche rapide.

Recherchez les indices associés aux points d'ancrage et de force.

Concevez une fonction qui fournit la connectivité de n'importe quel point de la grille pour n'importe quel modèle de connectivité donné.

Pour un nœud donné 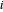, utilisez la connectivité pour déterminer les liens qui incluent ce nœud. Si les nœuds 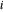et 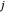sont reliés, alors 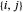et 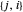représentent le même lien. Pour éviter les répétitions, considérez seulement celui avec .

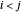Décrivez l'ensemble des liens par ℒ de sorte que, si un nœud 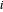et un nœud 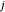forment un lien, alors .

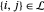Supposons que l'épaisseur d'un lien, et donc la masse par unité de longueur, doit être proportionnelle à la force qui sera exercée sur ce lien. Une façon pratique de décrire les liens dans ℒ est d'avoir une indexation des liens de sorte que, pour chaque paire 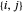connectée, il existe un index unique 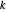avec .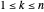

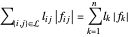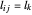L'objectif est de minimiser , où correspond à la longueur du lien entre les nœuds 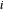et 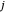avec index 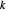, et 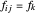correspond à la force exercée par le lien sur ses extrémités.

La fonction 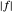est non linéaire, mais peut être exprimée comme une fonction linéaire en introduisan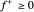t et 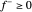de sorte que 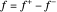et 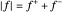. L'objectif est .

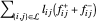À chaque nœud, excepté au point de force, aucune force externe n'est exercée.

Au point de force, une force unitaire verticale est exercée vers le bas.

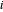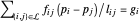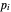À chaque nœud , non ancré, un équilibre des forces doit être établi , où correspond à la position du nœud 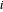, et 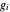correspond à la force externe au nœud 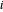. Définissez une fonction qui donne la contrainte d'équilibre des forces pour le nœud .

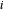Utilisez Complement pour éviter d'inclure les nœuds d'ancrage.

Les contraintes finales sont :

Résolvez le système qui en résulte.

Visualisez la poutrelle optimale avec des nuances de bleu indiquant la compression des liens et des nuances de rouge indiquant l'étirement des liens.