Optimisation de trajectoire
Minimisez 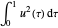 sous les contraintes de
sous les contraintes de 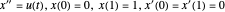 .
.
Cet exemple démontre comment un problème variationnel peut être discrétisé en un problème d'optimisation fini et résolu efficacement par des méthodes convexes, telles que QuadraticOptimization.
Le problème variationnel sera approximé en discrétisant le problème de la valeur limite et en utilisant la règle trapézoïdale à intégrer sur une grille uniformément espacée sur l'intervalle [0,1], 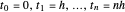 pour
pour 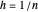 .
.
Supposons que la variable u[i] représente 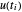 , et que x[i] représente
, et que x[i] représente 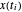 pour
pour 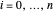 .
.
La contrainte de l'équation différentielle est facilement représentée à l'aide d'approximations de différence de second ordre centrées pour 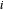 allant de 1 à
allant de 1 à 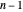 .
.
À la limite, les conditions de la dérivée zéro permettent l'utilisation de points fictifs  et
et 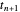 . Lorsque
. Lorsque  et
et 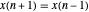 , la formule de différence de second ordre pour la première dérivée
, la formule de différence de second ordre pour la première dérivée 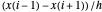 est égale à zéro pour
est égale à zéro pour 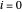 et
et 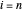 . Par conséquent, à la limite, utilisez ce qui suit :
. Par conséquent, à la limite, utilisez ce qui suit :
La règle trapézoïdale pour 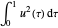 est donnée par ce qui suit.
est donnée par ce qui suit.
Puisque l'expression de la règle trapézoïdale est quadratique et que toutes les contraintes sont des contraintes d'égalité linéaire, le minimum de l'intégrale discrétisée peut être trouvé en utilisant directement QuadraticOptimization.
Les fonctions approximatives sont établies avec Interpolation.
Une solution analytique exacte, 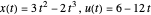 , est connue pour ce problème, il est donc possible de représenter l'erreur dans la discrétisation.
, est connue pour ce problème, il est donc possible de représenter l'erreur dans la discrétisation.
L'erreur asymptotique est d'à peu près 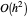 , donc en doublant
, donc en doublant 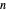 à 200 et en recalculant, l'erreur sera d'environ 1/4 de ce qui est montré ici.
à 200 et en recalculant, l'erreur sera d'environ 1/4 de ce qui est montré ici.
La solution analytique peut être trouvée en considérant une famille de courbes  où
où 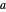 correspond à un paramètre. Cette courbe paramétrique satisfait aux conditions de limites prescrites
correspond à un paramètre. Cette courbe paramétrique satisfait aux conditions de limites prescrites  . Puisque
. Puisque 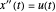 , on peut trouver un paramètre optimal
, on peut trouver un paramètre optimal 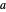 qui minimise
qui minimise 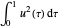 .
.
La valeur optimale de 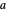 est à 2, ce qui correspond au résultat analytique
est à 2, ce qui correspond au résultat analytique 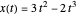 .
.