Problème de coupe maximum
Le problème de la coupe maximum détermine un sous-ensemble 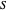 des sommets
des sommets 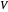 d'un graphe, pour lequel la somme des poids
d'un graphe, pour lequel la somme des poids 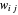 des arêtes, qui se croisent de
des arêtes, qui se croisent de 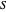 à son complément
à son complément 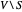 , est maximisée.
, est maximisée.
Cet exemple démontre comment SemidefiniteOptimization peut être utilisée pour mettre en place une fonction qui résout efficacement un relâchement du problème de coupe maximum du NP-complet.
Supposons que 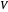 possède
possède 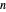 sommets pour qu'ils puissent être décrits par un index
sommets pour qu'ils puissent être décrits par un index 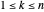 . Soit
. Soit 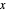 un vecteur avec des composantes
un vecteur avec des composantes 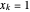 pour
pour  , et
, et 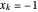 pour
pour 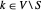 , de sorte que
, de sorte que 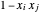 soit non nul (=2) seulement si
soit non nul (=2) seulement si 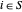 et
et 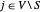 . Ainsi, la coupe maximum est trouvée en maximisant
. Ainsi, la coupe maximum est trouvée en maximisant 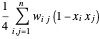 , où
, où 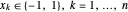 . L'objectif peut être réécrit comme tel :
. L'objectif peut être réécrit comme tel :
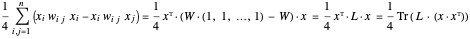
... où 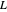 correspond à la matrice laplacienne du graphe et
correspond à la matrice laplacienne du graphe et 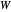 à la matrice d'adjacence pondérée.
à la matrice d'adjacence pondérée.
Pour les cas mineurs, le problème de la coupe maximum peut être résolu de manière exacte, mais cela n'est pas réalisable pour les plus grands graphes puisqu'en général le problème a une complexité NP-complet.
Le problème minimise 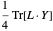 , où
, où 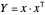 est une matrice semi-définie positive symétrique de rang 1, avec
est une matrice semi-définie positive symétrique de rang 1, avec 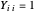 pour chaque
pour chaque 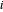 , ce qui équivaut à
, ce qui équivaut à 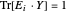 , où
, où 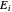 correspond à la matrice avec 1 à la position diagonale
correspond à la matrice avec 1 à la position diagonale 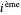 , et 0 partout ailleurs.
, et 0 partout ailleurs.
Pour rendre la solution réalisable, résolvez un problème relaxé où la condition de rang 1 est éliminée pour que cela ne requière que 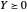 .
.
Le problème semi-défini en forme duale est donné par :
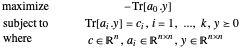
Elle est résolue à l'aide de SemidefiniteOptimization[c, {a0, a1, …, ak}, {"DualMaximizer" }].
Pour la solution 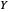 du problème de relaxation, on construit une coupure par arrondissement aléatoire : décomposez
du problème de relaxation, on construit une coupure par arrondissement aléatoire : décomposez 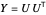 . Supposons que
. Supposons que 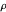 soit un vecteur aléatoire uniformément distribué de la norme unitaire et que
soit un vecteur aléatoire uniformément distribué de la norme unitaire et que 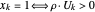 . Pour la démonstration, une fonction définie démontre la valeur de relaxation, la valeur arrondie et le graphe, avec les sommets
. Pour la démonstration, une fonction définie démontre la valeur de relaxation, la valeur arrondie et le graphe, avec les sommets 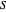 indiqués en rouge.
indiqués en rouge.
Trouvez une coupe maximum approximative à l'aide de la procédure montrée précédemment et comparez avec le résultat exact.
Déterminez la coupe maximum pour un graphe en grille.
Déterminez la coupe maximum pour un graphe aléatoire.
Comparez les temps pour les algorithmes relaxés et les algorithmes exacts sur un graphe de Peterson.